引入

由于不同层次存储设备访问速度的巨大差异，缓存（cache）在现代计算机系统结构起着至关重要的作用。缓存不仅仅指 CPU 的高速缓存，寄存器可以看作高速缓存的缓存，内存可以看作硬盘的缓存。在本文中，我们将讨论数据库系统的缓存策略，以 PostgreSQL 作为主数据库，Redis 作为 PostgreSQL 的缓存，还有一个中间层 DeTox 用于处理 clients 请求、并发控制、缓存控制等。

在大多数情况下，提高缓存对象的命中率（object hit rate）能够有效减少访问延迟，提高吞吐量。然而，单纯提高对象命中率对于数据库事务（transaction）型的工作负载来说是低效的，对象命中率的提高并不意味能够减少事务延迟。在本文中，我们将介绍 DeToX 缓存系统，一个利用事务依赖关系来做出替换和预取策略的缓存系统。DeToX 在实际工作负载和流行的 OLTP 基准测试中使事务命中率提高 1.3 倍，并将缓存效率提高 3.4 倍。

关键路径

在提出事务缓存和事务执行图之前，我们先引入一个概念：关键路径（critical path）。下面这段话摘自 CSAPP 3e 第 362 页：

作为分析在现代处理器上执行的机器级性能的一个工具，我们会使用程序的数据流（data-flow）表示，这是一种图形化的表示方法，展现了不同操作之间的数据相关是如何限制它们的执行顺序的。这些限制形成了图中的关键路径（critical path），这是执行一组机器指令所需时钟周期数的一个下界。

下面是一段 C 代码，使用 2 x 1 循环展开来计算浮点向量的积，其中 IDENT 是初始值。

/* 2 x 1 loop unrolling */
void combine5(vec_ptr v, data_t *dest) {
    long i;
    long length = vec_length(v);
    long limit = length - 1;
    data_t *data = get_vec_start(v);
    data_t acc = IDENT;

    /* Combine 2 elements at a time */
    for (i = 0; i < limit; i += 2) {
        acc = (acc * data[i]) * data[i + 1];   
    }

    /* Finish any remaining elements */
    for (; i < length; i++) {
        acc = acc * data[i];   
    }
    *dest = acc;
}

上述代码对应的 data-flow 如下图所示，%xmm0 保存累积变量 acc ，%rdx 保存循环变量 i，

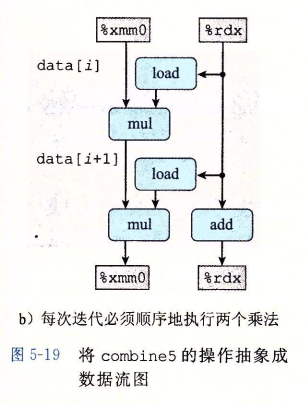
事实上，尽管使用了循环展开，由于数据依赖，每次循环内的两次乘法没法同时进行，关键路径上仍有 2 个 mul 操作，无法突破延迟界限。

如果我们增加累积变量，将一组合并运算分割成两个或更多的部分，并在最后合并结果来提高性能，代码修改后如下，

/* 2 x 2 loop unrolling */
void combine6(vec_ptr v, data_t *dest) {
    long i;
    long length = vec_length(v);
    long limit = length - 1;
    data_t *data = get_vec_start(v);
    data_t acc0 = IDENT;
    data_t acc1 = IDENT;

    /* Combine 2 elements at a time */
    for (i = 0; i < limit; i += 2) {
        acc0 = acc0 * data[i];
        acc1 = acc1 * data[i + 1];   
    }

    /* Finish any remaining elements */
    for (; i < length; i++) {
        acc0 = acc0 * data[i];   
    }
    *dest = acc0 * acc1;
}

修改后的代码对应的 data-flow 如下，

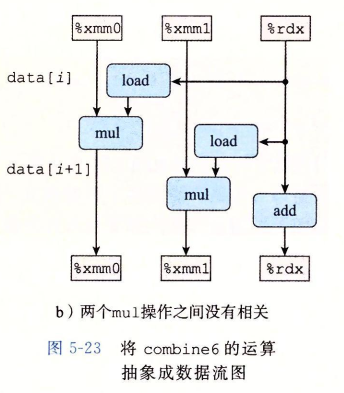
可以看到，两个 mul 操作之间没有了数据依赖，关键路径上仅有 1 个 mul 操作。优化后的代码突破了延迟界限，效率提升了 1 倍。

实际上关键路径对应了“最长路径”，代表了执行耗时最长的计算路径，这和“木桶原理”类似，唯有减少关键路径的长度才能提高执行效率。其实事务的执行图也类似于数据流图，我们可以从中获得启发，通过分析和减少关键路径长度来提高事务的执行效率。

事务执行图

事务是由应用发出的以原子方式读取和写入请求组成。其中一些操作是可以独立并行地执行，而其他操作则依赖于前面操作的结果。实际上，事务执行可以通过操作的 DAG 来描述。

下面是一段 SQL 代码，

begin;
a = SELECT A.a FROM A; 
b = SELECT B.b FROM B WHERE B.a = a; 
c = SELECT C.c FROM C WHERE C.a = a;
d = SELECT D.d FROM D WHERE D.c = c;
commit;

将上述的事务执行图可以抽象成如下 DAG。图中的每个顶点代表对一个 table 的一次 read 或者 write 操作（由于顶点是缓存的基本对象，在后文会把顶点称作 key），图中的边代表依赖关系。例如上面代码中先在 A 表中查询得到中间结果 a，再在 B 表中根据 a 进行二次查询，后一次查询依赖前一次的查询结果。有依赖关系的查询只能顺序执行，而没有依赖关系的查询可以并发执行，例如 b 和 c 的查询。

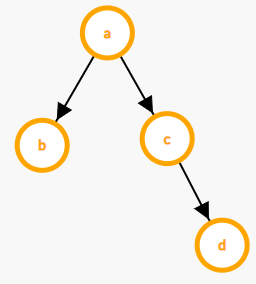
NOTE 1：我们是在编译时分析出整个执行图的结构，在单次事务运行时可能仅会访问其中一个子图。在上面的例子中，省略了一些 if 条件判断的代码，比如仅在 a 不为空时才查询 B。因此在运行时，并不是每一次都会遍历 a, b, c, d 四个顶点，可能仅遍历 a 或者 a, b 或者 a, c 等。这也导致了不同的顶点会有不同的访问频率。

NOTE 2：关于写操作，写操作会先在 DeTox 这个中间层缓冲，直到事务 commit 后所有写入都直接写到主数据库持久化。因此，写操作均可视为缓存命中，在本文的例子中我们仅讨论读操作。

现有方法存在的问题

Case 1

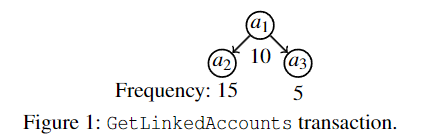
例如图 1，我们考虑一个最简单的事务 GetLinkedAccounts（查询相关账户），它返回与主账户 $a_1$ 关联的辅助银行账户 $a_2$ 和 $a_3$。如果我们仅缓存 $a_1$，可以减少事务延迟。然而不幸的是，单独缓存 $a_2$ 或 $a_3$ 却不能减少事务延迟。（注：图中的数字代表访问频率）

事务在对象上具有隐含的 “all-or-nothing”属性，这是传统缓存算法无法捕捉到的。考虑这样的情况：缓存仅能存储 $a_1 \sim a_3$ 中的任意其一，在事务访问中，$a_2$ 的访问频率远高于 $a_1$ 和 $a_3$ ，LFU 和 LRU 会选择缓存 $a_2$（而不是 $a_1$），从而导致事务延迟没有改善。事实上，最优选择应该是缓存 $a_1$。

Case 2

除了经典的 LFU 和 LRU 算法，我们再来考虑一下理论最优算法 Belady，它每次在 evict 的时候会选择下一次访问时间最远的对象。由于该算法需要预先知道访问序列，所以是无法实现的，理论最优算法。

考虑如下情况，每次事务同时访问 3 个 key，

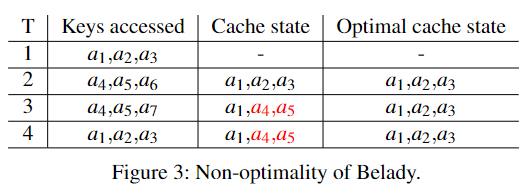
从上图结果可以看出，即使是理论最优算法 Belady，也并不能做出最大化事务命中率的最佳决策。

NOTE：作者还在论文附录中提出了 Transactional Belady 算法，即基于事务的 Belady 算法。该算法的提出很符合直觉，但是很遗憾的是该算法也被证明不能做出最佳决策。

事务缓存

从事务执行图中可以发现，事务的延迟是由其关键路径的长度（critical length）或最长的非缓存路径上顺序访问的数量决定（即 DAG 的最长路，不包括缓存的节点，这是一个经典问题，可以通过 DP 在 $\mathcal O(n)$ 内求得）。

NOTE：由于缓存对象与非缓存对象访问速度的巨大差异，为了简单起见，我们认为缓存对象提供的请求具有零延迟（zero latency）。在此模型下，事务延迟由顺序、非缓存访问的数量定义。

在上图的例子中，在未缓存的情况关键路径长度为 3，如果我们缓存了 a 或 d，关键路径长度减少为 2，在这里，我们把关键路径长度每减少 1 定义为 1 次事务缓存命中（a transactional hit，后文为方便简称为缓存命中），把缓存后的关键路径长度与未缓存的关键路径长度的比值定义为事务缓存命中率（transactional hit rate，THR）。例如，同时缓存 {a, b, c} 将产生 2 次事务缓存命中，THR 为 $\dfrac{2}{3} = 66.7\%$。

分组与评分

DeTox 整个算法流程如下：在编译期通过静态分析得到事务执行图，在运行期根据应用的请求，对每个组和键进行打分，根据得分来做出相应的缓存策略（保留得分高的，驱逐得分低的）。关于压缩组和 levels 两个优化将在下节讨论。

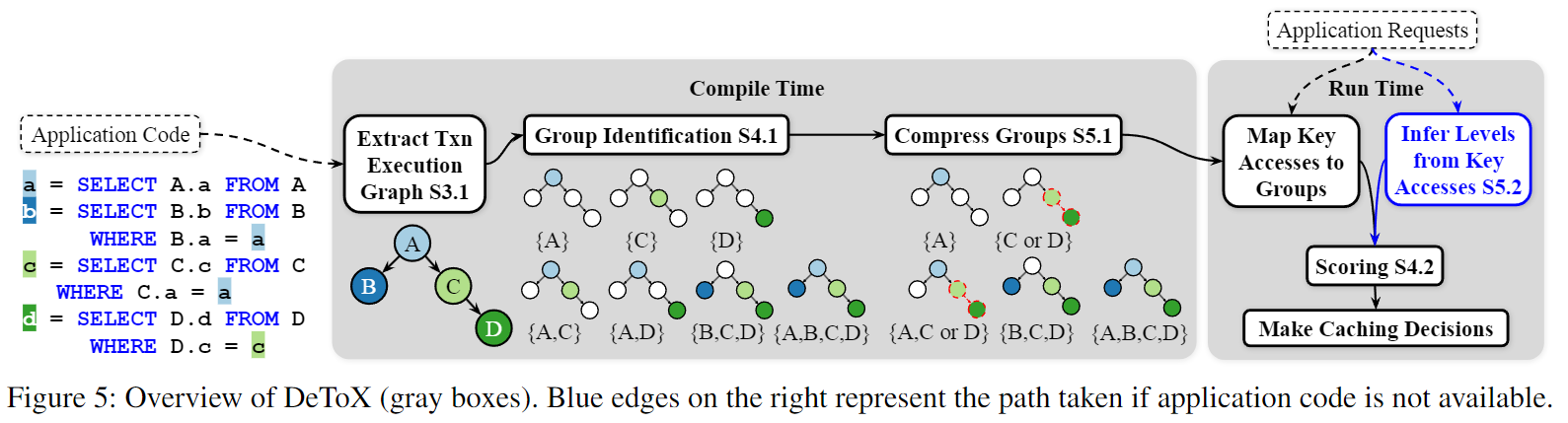
打分（scoring）总共分为下面 3 个步骤：

先给出一张各个打分参数的解释表：

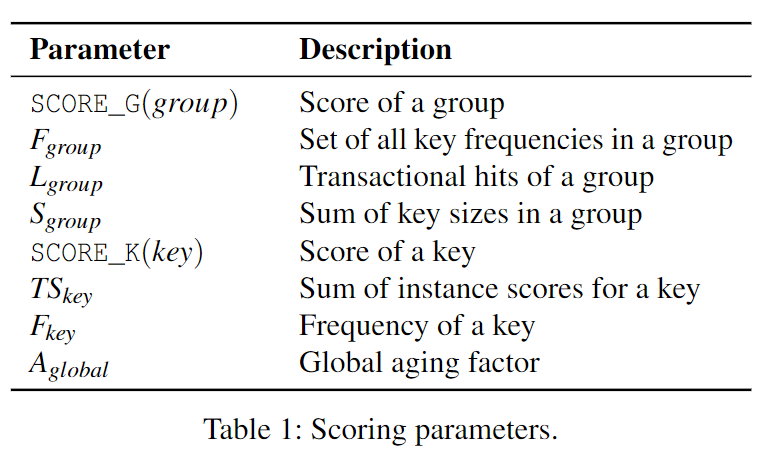
以及论文中的一张 example 图，在后面的介绍都以下图的例子进行讲解，

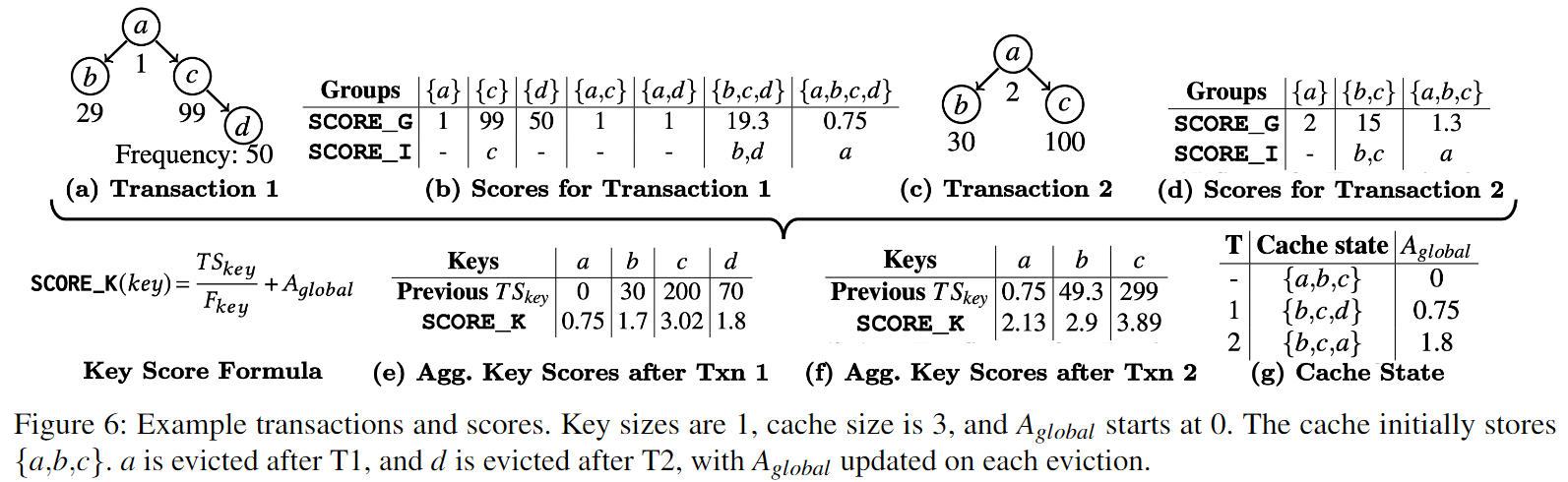
分组

在编译期，我们需要根据执行图进行分组（group indetification）。我们把满足下面两个条件的 key 集合称为一个完备组（complete group，以下简称“组”）：

• 缓存该组能够减少关键路径长度
• 从组内移除任意 key 都会导致关键路径长度的增加

例如 Figure 6 中的 Txn 1，{a}, {c}, {a, d} 等都是一个个的组，但 {c, d} 不是一个组，因为缓存 {d} 与 {c, d} 的关键路径长度相等。

组打分

第一轮，我们对每个组进行打分，得到 $\mathtt{SCORE_G}$。

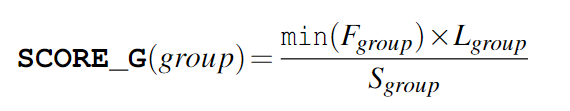
对于该计算公式可以这样理解，组内频率最低的 key 决定了整个组的 cacheability，频率越高越好。$L_{group}$ 表示关键路径减少的大小，即事务缓存命中数，缓存命中越多越好。$S_{group}$ 表示需要的缓存大小，由于 cache 是有限的，占用的缓存当然越少越好。

例如 Txn 1，组 ${a, b, c, d}$，它的 score 是 $\dfrac{\min\{1, 29, 99, 50\}\times 3}{4} = 0.75$。

键赋分

在这一轮，我们在单个事务范围内对每个 key 进行打分，得到 $\mathtt{SCORE_I}$。I 代表 instance，表示一个 key 在单个事务实例的得分。

首先找到评分最高的组，将该组中的所有 key 的分赋值为该组的分。然后寻找是该组超集（superset）且得分最高的组，将组内未被赋分的 key 赋值为该组得分。重复迭代以上算法，直至该事务访问的所有 key 都被赋分。

例如，在 Figure 6 图 b 中，得分最高的组是 {c}，则 c 的分赋为 99。然后我们认为得分最高的组是应该会被放入到缓存中的，接下来我们考虑再缓存哪些组能够进一步增加事务缓存命中，我们考虑当前组的超集，超集一定能够增加缓存命中。在这里，{c} 的超集组有 {a, c}，{b, c, d} 和 {a, b, c, d}，得分最高的是 {b, c, d}，因此我们把未赋分的 b, d 赋分为 19.3。{b, c, d} 的超集只有 {a, b, c, d} 了，因此 a 被赋分为 0.75。由于全集一定是一个组，且它是其它任意集合的超集，所以每个被访问的 key 都会被赋分。

NOTE：为什么我们是寻找超集，而不是直接按照组的分数从大到小对键进行赋分呢？因为缓存当前组的超集一定能够增加缓存命中，缓存其它组并不一定会增加缓存命中。例如我们在缓存了 {c} 的基础上，再缓存 {d}，关键路径长度不变。

跨事务综合打分

最后一轮，我们综合多次事务实例，计算 key 的最终得分。

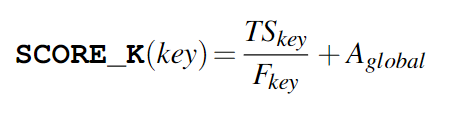
$TS_{key}$ 代表该 key 在目前所有事务实例中的总得分，$F_{key}$ 代表 key 的访问频率，两者的比值可以理解为每次访问带来的平均得分（对缓存命中的平均贡献）。$A_{global}$ 是全局老化因子，初始值为 $0$，每次在 evict 一个 key 后 $A_{global}$ 被赋值为该 key 的 $\mathtt{SCORE_K}$。这样做可以避免热键在过去访问频率很高，得分很高长期占据缓存，阻碍近期新活跃的键进入缓存。新活跃的键在加上 $A_{global}$ 后至少会比被 evict 的键分数要高，从而有机会进入缓存。

NOTE：可能读者会有疑问，每个 $\mathtt{SCORE_K}$ 在计算的时候都加上一个相同的 $A_{global}$，这对比较相对大小有什么用呢？注意，只有当前访问的 key 才会计算新的 $\mathtt{SCORE_K}$，其余的 key（当前未活跃的） 的 $\mathtt{SCORE_K}$ 保持不变。

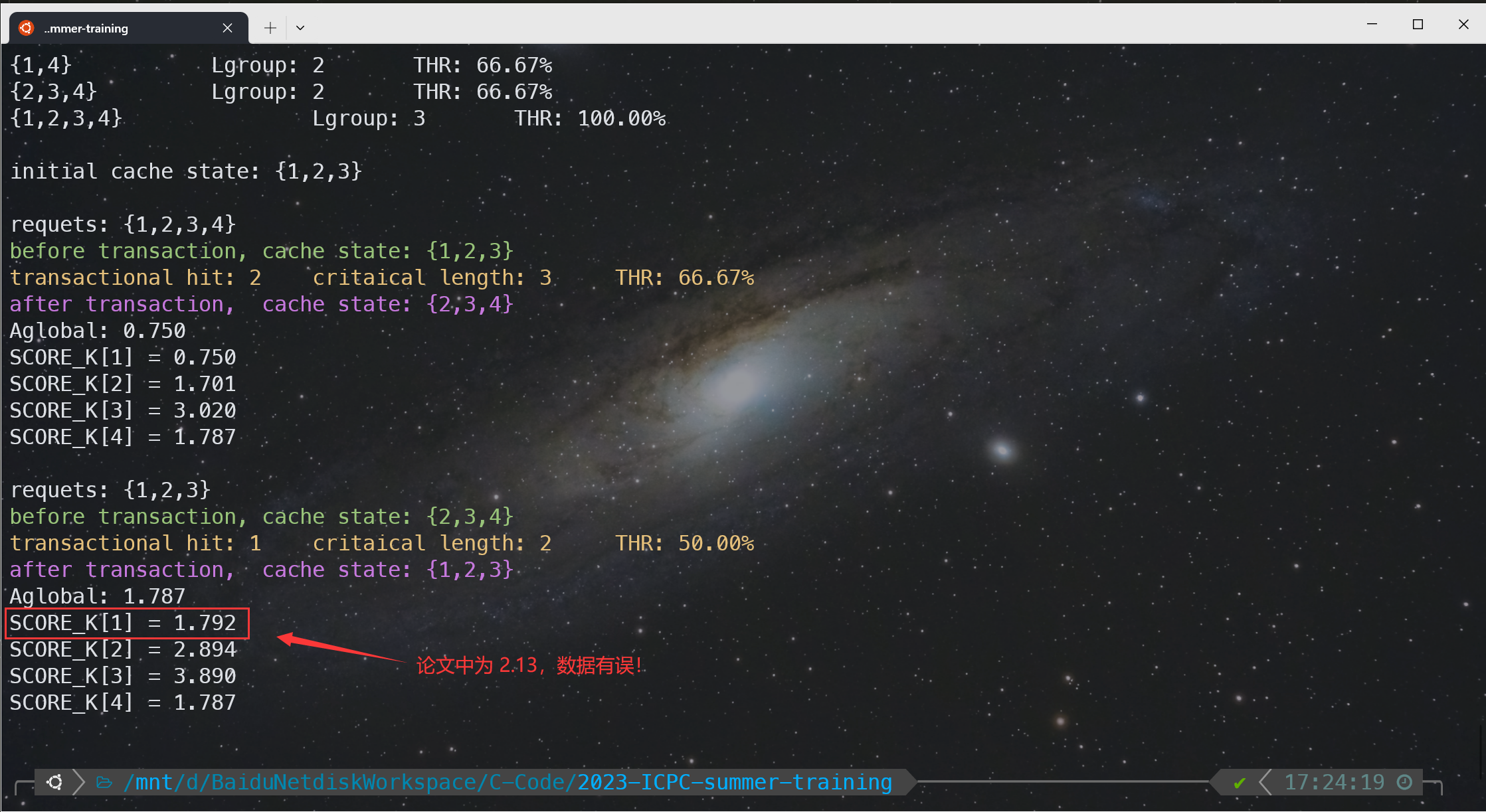
例如 Txn 2，$\mathtt{SCORE_K(c)} = \dfrac{299 + 15}{100} + 0.75 = 3.89$。但是很让笔者不解的是，经过多次验算，论文中 Txn 2 中 $\mathtt{SCORE_K(a)}$ 的数据是错误的！正确结果应该是 $\dfrac{0.75+1.3}{2} + 0.75 = 1.792$，该结果也在后面的代码模拟中得到了验证。（经过试验，论文中应该是把 a 的 $\mathtt{SCORE_I}$ 当成了 2 来计算，$\dfrac{0.75+2}{2} + 0.75 = 2.125$ 恰好符合文中的 2.13）

算法优化

目前的 DeToX 算法面临两个主要问题：

1. 组的数量随 key 增加呈指数级增长
2. 在一些情况下不一定能够得到 application code

针对上述两个问题，论文提出了可交换组和 levels 两个优化办法来解决。

NOTE：最坏情况下如果 DAG 是一条链，那么任意 key 的集合都是一个组，会有多达 $2^n$ 个组

可交换组

对于事务的拓扑结构，其完备组的数量呈指数级，如果对所有完备组进行打分，会需要很长时间。

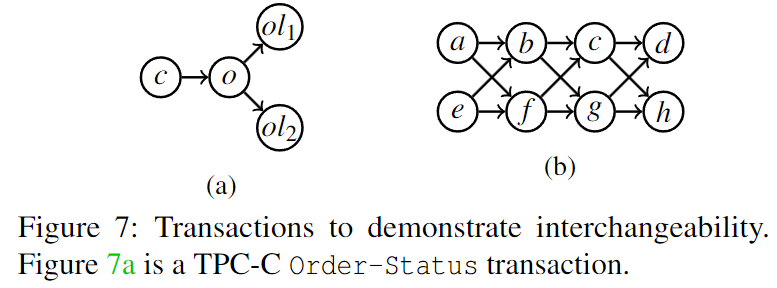
可交换组的概念定义稍微复杂些，具体详见论文。简单来说，如果 A 和 B 互为可交换组，那么对于任意包含 A 的完备组，把里面的 A 替换为 B，仍然是一个完备组，且 transaction hit 相同。例如上图中 (a) 的所有完备组为：{c}, {o}, {ol1, ol2}, {c, o}, {o, ol1, ol2}, {c, ol1, ol2}, {c,o,ol1,ol2}。其中 {c} 和 {ol1, ol2} 互为可交换组。

我们可以在编译期找到所有的可交换组，从而对所有完备组进行压缩，在评分时仅仅只考虑压缩组。例如上图（b），{a ,e}, {b, f}, {c,g}, {d, h} 两两互为可交换组，我们把 {a ,e}, {b, f}, {c,g}, {d, h} 记作 [C]。那么对于大小为 4 的组可以表示成 [C, C]，大小为 6 的组可以表示成 [C, C, C]，大小为 8 的组可以表示为 [C, C, C, C]。在运行时，假设这些可交换组的 $\mathtt{SCORE_G}$ 分别为：{a, e} : 1, {b, f } : 10, {c, g} : 30, {d, h} : 50。那么在对形如 [C, C] 这样的组进行打分的时候，我们可以知道分最高的一定是 {d, h, c, g}，这是因为 $\mathtt{SCORE_G}$ 在计算的时候，可交换组的 $L_{group}$ 和 $S_{group}$ 都相同，$\mathtt{SCORE_G}$ 仅仅取决于 $\mathtt{SCORE_G}$ 。

Levels

在无法得到 application code 的情况下，我们使用 levels 方法在运行时动态推断完备组。levels 的思想很简单，我们把同时并行请求的 keys 当作一个 level ，把它们视为一个完备组或者可交换组。

例如 Figure 6a，在执行时，会依次并发请求 {a}, {b, c} 和 {d}，据此我们就把 {a}, {b, c} 和 {d} 当作 3 个组，并按照前面的方法进行计算打分。

尽管我们得到的 level 可能只是所有完备组的子集，因此这个方法可能导致次优解，但在实际测试中，它与前两者拥有相同的缓存效果。

代码实现

笔者花了两天时间用 cpp 简单实现了一个基于 DeTox 的事务缓存模拟器（Transaction Cache Simulator），输入执行图 DAG、缓存大小、每次的 requests 等信息，输出缓存状态、事务缓存命中率等。不得不吐槽作者在 DeToX 算法很多地方仅仅做了描述性的介绍，没有给出伪代码或者具体算法流程，这也导致了我的代码量（接近 300 行）比想象的多了不少（两个优化还没有实现）。

由于作者没有在很多地方没有给出算法的具体实现，所以这些地方的算法我根据定义和描述自己设计的，可能存在很多待优化的空间，下面我简单讲讲算法思路：

• DAG 不一定连通：添加虚拟节点 0 号点作为整个 DAG 的起点，0 号点向每个入度为 0 的点连边

• 计算所有完备组：直接 $\mathcal O(2^n)$ 枚举所有可能的组，然后 $\mathcal O(n)$ 在 DAG 上做个记忆化搜索 / DP 求出最长路（即 critical length）。不必再枚举一个组的子集来 check 当前组是不是完备组，只需要考虑从组里面剔除 1 个 key，得到的组的 critical length 是不是比当前大就行了。从小到大枚举组，这样组的子集就已经计算过了，具体见代码。

• 子图：由于 requests 不同，实际的执行图是 DAG 的子图，而不幸的是，子图与原图的分组并无直接关系，这要求我们还得计算出所有合法子图的完备组。这部分需要枚举子集，复杂度为 $\mathcal O(3^n)$。
• 状态压缩：对缓存状态和组的表示均使用二进制状态压缩，便于进行集合的数学运算
• 超集：在第二轮打分的时候，需要知道超集，这部分在计算完备组的时候也需要预处理出来，即计算出每个完备组的超集是哪些完备组

总时间复杂度为 $\mathcal O(n\cdot 3^n + T\cdot n\log n)$，空间复杂度为 $\mathcal O(n\cdot 3^n)$

输入示例如下（实际输入时请去掉注释）：

4 3 3           // 点数 边数 cache大小
1 2
1 3
3 4
1 1 1 1         // key的大小
0 28 98 49      // 初始的访问频率
0 30 200 70     // 初始的 totalScore
3 1 2 3         // 初始缓存状态
2               // 模拟的请求数
4 1 2 3 4
3 1 2 3

运行效果如下：

$ ./TraCheSimulator < data.in                                                           
subgraph: {1}
critical length: 1
complete group:
{1}             Lgroup: 1       THR: 100.00%

subgraph: {1,2}
critical length: 2
complete group:
{1}             Lgroup: 1       THR: 50.00%
{2}             Lgroup: 1       THR: 50.00%
{1,2}           Lgroup: 2       THR: 100.00%

subgraph: {1,3}
critical length: 2
complete group:
{1}             Lgroup: 1       THR: 50.00%
{3}             Lgroup: 1       THR: 50.00%
{1,3}           Lgroup: 2       THR: 100.00%

subgraph: {1,2,3}
critical length: 2
complete group:
{1}             Lgroup: 1       THR: 50.00%
{2,3}           Lgroup: 1       THR: 50.00%
{1,2,3}         Lgroup: 2       THR: 100.00%

subgraph: {1,3,4}
critical length: 3
complete group:
{1}             Lgroup: 1       THR: 33.33%
{3}             Lgroup: 1       THR: 33.33%
{1,3}           Lgroup: 2       THR: 66.67%
{4}             Lgroup: 1       THR: 33.33%
{1,4}           Lgroup: 2       THR: 66.67%
{3,4}           Lgroup: 2       THR: 66.67%
{1,3,4}         Lgroup: 3       THR: 100.00%

subgraph: {1,2,3,4}
critical length: 3
complete group:
{1}             Lgroup: 1       THR: 33.33%
{3}             Lgroup: 1       THR: 33.33%
{1,3}           Lgroup: 2       THR: 66.67%
{4}             Lgroup: 1       THR: 33.33%
{1,4}           Lgroup: 2       THR: 66.67%
{2,3,4}         Lgroup: 2       THR: 66.67%
{1,2,3,4}               Lgroup: 3       THR: 100.00%

initial cache state: {1,2,3}

requets: {1,2,3,4}
before transaction, cache state: {1,2,3}
transactional hit: 2    critaical length: 3     THR: 66.67%
after transaction,  cache state: {2,3,4}
Aglobal: 0.750
SCORE_K[1] = 0.750
SCORE_K[2] = 1.701
SCORE_K[3] = 3.020
SCORE_K[4] = 1.787

requets: {1,2,3}
before transaction, cache state: {2,3,4}
transactional hit: 1    critaical length: 2     THR: 50.00%
after transaction,  cache state: {1,2,3}
Aglobal: 1.787
SCORE_K[1] = 1.792
SCORE_K[2] = 2.894
SCORE_K[3] = 3.890
SCORE_K[4] = 1.787

Code：

/*** 
 * @brief 基于 DeTox 的事务缓存模拟器（Transaction Cache Simulator）
 * @author LRL52
 * @date 2023-11-09 ~ 2023-11-10
 */
#include <algorithm>
#include <cassert>
#include <cstddef>
#include <format>
#include <iostream>
#include <vector>
int n, m, cacheSize, cacheState, curCacheSize;
double Aglobal;
std::vector<std::vector<int> > Graph, Lgroup, Sgroup, groupBin;
std::vector<std::vector<double> >SCORE_G;
std::vector<std::vector<std::vector<int> > > group, superset;
std::vector<int> size, freq, criticalLength;
std::vector<double> SCORE_I, SCORE_K, totalScore;

void dfs1(int x, int S, int &_S, std::vector<int> &inSet) {
    if (x != 0) {
        _S |= 1 << (x - 1);
        inSet.push_back(x);
    }
    for (auto v : Graph[x]) {
        if (S >> (v - 1) & 1) {
            dfs1(v, S, _S, inSet);
        }
    }
}

int dfs2(int x, std::vector<int> &f, const std::vector<int> &w) {
    if (f[x] != -1) return f[x];
    f[x] = w[x];
    for (auto v : Graph[x]) {
        f[x] = std::max(f[x], dfs2(v, f, w) + w[x]);
    }
    return f[x];
}

// O(n * 2^n) 计算所有完备组
void calcCompleteGroup(int S) {
    std::vector<int> inSet;
    int _S = 0;
    dfs1(0, S, _S, inSet);
    if (_S == 0 || _S != S) return;
    // 枚举子集
    std::vector<int> subset;
    for (int i = S; i; i = (i - 1) & S) {
        subset.push_back(i);
    } 
    subset.push_back(0);
    std::reverse(subset.begin(), subset.end());
    int rest = ((1 << n) - 1) ^ S, sizeSum = 0;
    std::vector<int> w(n + 1), L(1 << n);
    for (auto i : subset) {
        std::vector<int> s, f(n + 1, -1);
        for (int j = 1; j <= n; ++j) w[j] = 1;
        sizeSum = 0;
        for (int j = 0; j < n; ++j) { 
            if ((i | rest) >> j & 1) {
                w[j + 1] = 0;
            }
            if (i >> j & 1) {
                s.push_back(j + 1);
                sizeSum += size[j + 1];
            }
        }
        dfs2(0, f, w);
        L[i] = f[0];
        if (i == 0) criticalLength[S] = f[0];
        int ok = 1;
        for (int j = 0; j < n; ++j) {
            if (i >> j & 1) {
                int k = i ^ (1 << j);
                if (L[k] <= L[i]) {
                    ok = 0;
                    break;
                }
            }
        }
        if (ok && i) {
            group[S].push_back(std::move(s));
            Lgroup[S].push_back(criticalLength[S] - L[i]);
            Sgroup[S].push_back(sizeSum);
            groupBin[S].push_back(i);
        }
    }
    SCORE_G[S].resize(group.size());
    // 计算每个组的 “超集”
    for (auto s : groupBin[S]) {
        std::vector<int> sup;
        for (size_t i = 0; i < groupBin[S].size(); ++i) {
            int t = groupBin[S][i];
            if ((s | t) == t && s != t) {
                sup.push_back(i);
            }
        }
        superset[S].push_back(std::move(sup));
    }
}

void calcTranHit(int S) {
    std::vector<int> f(n + 1, -1), w(n + 1);
    int rest = ((1 << n) - 1) ^ S;
    for (int j = 1; j <= n; ++j) w[j] = 1;
    for (int j = 0; j < n; ++j) { 
        if ((cacheState | rest) >> j & 1) {
            w[j + 1] = 0;
        }
    }
    int L = dfs2(0, f, w), criticalL = criticalLength[S];
    std::cout << "\033[33m" <<
                std::format("transactional hit: {}\tcritaical length: {}\tTHR: {:.2f}%\n", criticalL - L,
                criticalL, (double)(criticalL - L) / criticalL * 100.0)
              << "\033[0m";
}


// 模拟事务请求后的缓存策略
void simulator(int S, const std::vector<int> &s) {
    if (group[S].size() == 0) {
        std::cerr << "Error: invalid requests!\n";
        return;
    }
    calcTranHit(S);
    for (auto x : s) ++freq[x];
    for (size_t i = 0; i < group[S].size(); ++i) {
        auto &g = group[S][i];
        auto Fgroup = freq[g[0]];
        for (auto x : g) Fgroup = std::min(Fgroup, freq[x]);
        SCORE_G[S][i] = (double)Fgroup * Lgroup[S][i] / Sgroup[S][i]; // 每个 group 打分
    }
    int cnt = 0, idx = 0;
    for (size_t i = 0; i < group.size(); ++i) {
        if (SCORE_G[S][i] > SCORE_G[S][idx])
            idx = i;
    }
    for (int i = 1; i <= n; ++i) SCORE_I[i] = 0.0;
    for (auto x : group[S][idx]) {
        SCORE_I[x] = SCORE_G[S][idx]; // 根据每个 group 的分对每个 key 赋分
        ++cnt;
    }
    while (cnt < (int)s.size()) {
        int nxt = -1;
        for (auto i : superset[S][idx]) {
            if (nxt == -1 || SCORE_G[S][i] > SCORE_G[S][nxt]) {
                nxt = i;
            }
        }
        assert(nxt != -1);
        idx = nxt;
        for (auto x : group[S][idx]) {
            if (SCORE_G[S][idx] > SCORE_I[x]) {
                SCORE_I[x] = SCORE_G[S][idx]; // 根据每个 group 的分对每个 key 赋分
                ++cnt;
            }            
        }
    }
    for (auto x : s) {
        totalScore[x] += SCORE_I[x];
        SCORE_K[x] = totalScore[x] / freq[x] + Aglobal; // 根据公式，计算每个 key 的最终得分 
    }
    std::vector<int> order;
    for (int i = 1; i <= n; ++i) order.push_back(i);
    std::sort(order.begin(), order.end(), [](const int &t1, const int &t2) {
        return SCORE_K[t1] > SCORE_K[t2];
    });
    int newCacheState = 0; curCacheSize = 0;
    for (auto x : order) {
        if (curCacheSize + size[x] <= cacheSize) {
            newCacheState |= 1 << (x - 1);
            curCacheSize += size[x];
        }
    }
    int evictSet = cacheState & (~newCacheState);
    for (int i = 0; i < n; ++i) {
        if (evictSet >> i & 1) {
            Aglobal = std::max(Aglobal, SCORE_K[i + 1]);
        }
    }
    cacheState = newCacheState;
}

void printVector(const std::vector<int> &output) {
    std::cout << "{";
    for (size_t i = 0; i < output.size(); ++i)
        std::cout << output[i] << ",}"[i + 1 == output.size()];
}

void printBinary(int S) {
    std::vector<int> output;
    for (int i = 0; i < n; ++i) {
        if (S >> i & 1)
            output.push_back(i + 1);
    }
    printVector(output);
}

int main() {
    std::ios::sync_with_stdio(false);
    std::cin.tie(nullptr);

    std::cin >> n >> m >> cacheSize;
    Graph.resize(n + 1);
    size.resize(n + 1), freq.resize(n + 1), totalScore.resize(n + 1);
    SCORE_I.resize(n + 1), SCORE_K.resize(n + 1);
    Lgroup.resize(1 << n), Sgroup.resize(1 << n), group.resize(1 << n), groupBin.resize(1 << n);
    SCORE_G.resize(1 << n), superset.resize(1 << n), criticalLength.resize(1 << n);
    for (int i = 1; i <= m; ++i) {
        int x, y;
        std::cin >> x >> y;
        Graph[x].push_back(y);
    }
    for (int i = 1; i <= n; ++i) std::cin >> size[i];
    for (int i = 1; i <= n; ++i) std::cin >> freq[i];
    for (int i = 1; i <= n; ++i) std::cin >> totalScore[i];
    int K;
    std::cin >> K;
    for (int i = 1; i <= K; ++i) {
        int x;
        std::cin >> x;
        curCacheSize += size[x];
        cacheState |= 1 << (x - 1);
    }

    std::vector<int> deg(n + 1);
    for (int x = 1; x <= n; ++x) {
        for (auto y : Graph[x]) {
            ++deg[y];
        }
    }
    for (int i = 1; i <= n; ++i) {
        if (!deg[i]) {
            Graph[0].push_back(i); // 添加 0 号点作为执行图的起始点
        }
    }
    for (int S = 0; S < 1 << n; ++S) {
        calcCompleteGroup(S);
        if (group[S].size() == 0) continue;
        std::cout << "subgraph: {";
        auto &subgraph = group[S].back();
        printVector(subgraph);
        std::cout << "\n";
        std::cout << std::format("critical length: {}\n", criticalLength[S]);
        std::cout << "complete group: " << "\n";
        for (size_t i = 0; i < group[S].size(); ++i) {
            auto &s = group[S][i];
            printVector(s);
            std::cout << std::format("\t\tLgroup: {}\tTHR: {:.2f}%\n", Lgroup[S][i], \
                        (double)Lgroup[S][i] / criticalLength[S] * 100.0); 
        }
        std::cout << "\n";
    } 

    std::cout << "initial cache state: ";
    printBinary(cacheState);
    std::cout << "\n\n";

    std::cin >> K;
    for (int i = 0; i < K; ++i) {
        int k, x, S{};
        std::vector<int> s;
        std::cin >> k;
        for (int j = 1; j <= k; ++j) {
            std::cin >> x;
            s.push_back(x);
            S |= 1 << (x - 1);
        }
        std::cout << "requets: ";
        printBinary(S);
        std::cout << "\n";
        std::cout << "\033[92m" << "before transaction, cache state: ";
        printBinary(cacheState);
        std::cout << "\n" << "\033[0m";
        simulator(S, s);
        std::cout << "\033[95m" << "after transaction,  cache state: ";
        printBinary(cacheState);
        std::cout << "\033[0m" << std::format("\nAglobal: {:.3f}\n", Aglobal);

        for (int j = 1; j <= n; ++j)
            std::cout << std::format("SCORE_K[{}] = {:.3f}\n", j, SCORE_K[j]);
        std::cout << "\n";
    }

    return 0;
}