CSAPP Lab：Cache Lab
|
|
1,664
|
0
|
CSAPP
|
admin52

3302 字
|
30 分钟
本文最后更新于 339 天前，内容如有失效请评论区留言。

[toc]

做完 Performance Lab 后，摆了一两天玩 PVZ2，又继续来做 Cache Lab。刚跑通本 Lab 的 Part A，某老师就让第二天内交编译的 Lab4，于是第二天花了一整天速成了 Lab4。之后又边摆边做用了两天才搞完这个 Cache Lab。

Cache Lab 介绍

本次实验分为 PartA 和 PartB 两部分。PartA 要求写一个小的 C 程序（官方估算 200 ~ 300 行，实际我完整实现大约 140 行）实现缓存模拟器。PartB 要求对矩阵转置程序进行优化，将 cache miss 降到最少。本实验将帮助你理解 cache 的工作机制，以及它对程序性能的影响。

? cachelab-handout.tar

? cachelab.pdf

? rec07.pdf

? waside-blocking.pdf

这个实验的材料稍微多一点，除了文档和实验包之外，rec07.pdf 是实验介绍的 PPT（我才发现其实每个实验都有 PPT 的介绍，也是 CMU 的 course，后文有链接可以找到），waside-blocking.pdf 是一篇关于分块矩阵加速矩阵乘法的文章，也推荐看看。

首先解压实验包：

tar xvf cachelab-handout.tar

image-20230101162229657

实验会用到 valgrind 内存分析与泄露检测工具，

sudo apt install valgrind
valgrind --log-fd=1 --tool=lackey -v --trace-mem=yes ls -l

按照文档的介绍使用试试，

image-20230101163943528

Part A：缓存模拟器

为了让你能确确实实理解缓存的运行机制，你需要写一个缓存模拟器。hit 和 miss 书上都有，分别表示缓存命中和不命中，eviction 表示“驱逐，收回”的意思，因此当发生缓存替换的时候就会出现 eviction，把已有的缓存“驱逐”走。输入数据是 valgrind 生成的 .trace 文件，输出hit、miss、eviction 的次数（不用考虑 i-cache，只需要计算 d-cache，eviction 的时候使用 LRU 替换策略 ）。csim-ref 是提供的标准程序，做成和它一样即可，建议最好支持 -v 选项可以观察每一条指令的具体情况。下面是 csim-ref 的使用示例：

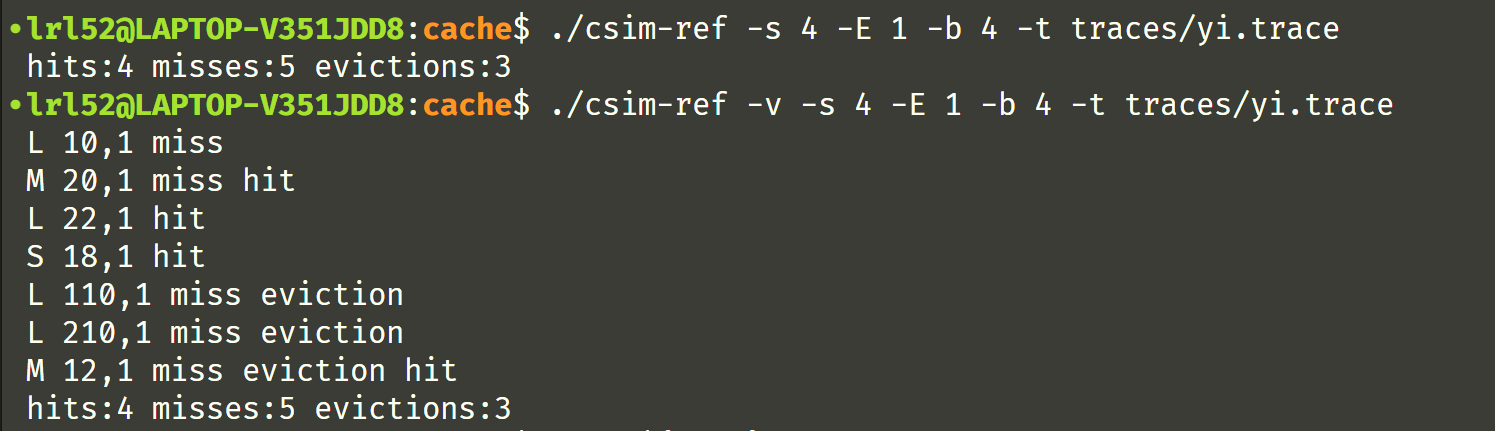
image-20230101165524282

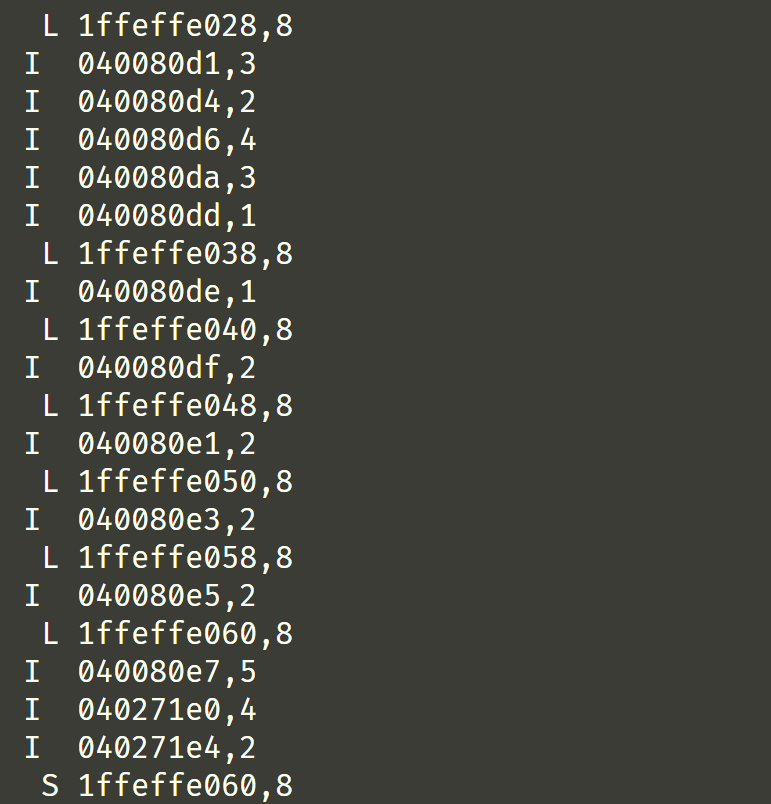
一开始对这句话比较懵逼，后来要写代码就懂了，这句话的意思是每次访存的 size 是不会超过一个缓存 block 的大小的，因此像 L 04f6b868,8 这种指令的最后一个 8 就可以忽略掉，

image-20230101180935853

这是期望的测试结果，每次会给不同的 (s, E, b) 来模拟，

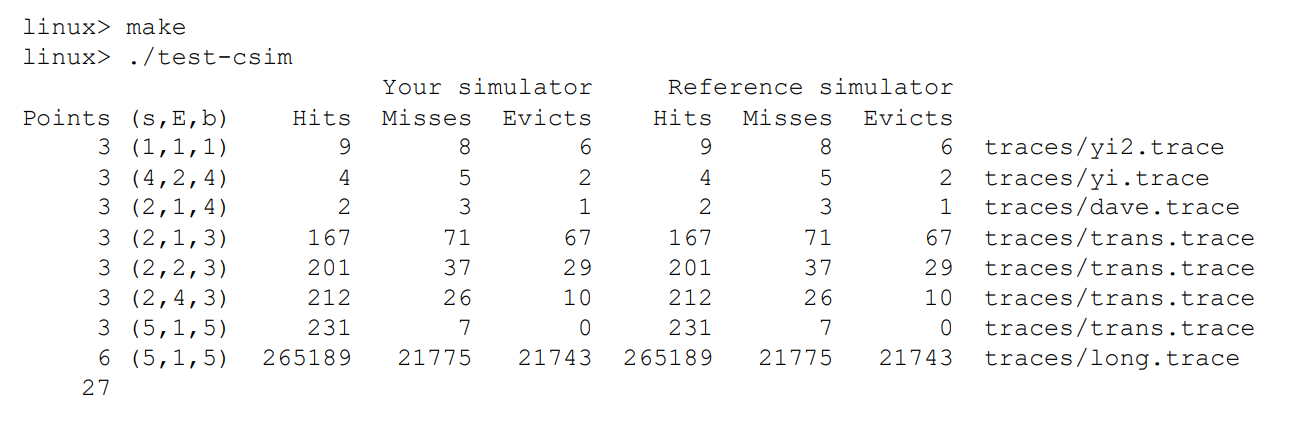
image-20230101201909765

为了更好的解析 Linux 命令行参数，文档建议使用 getopt 库函数，下面是学习参考过的 blog：

Linux下getopt()函数的简单使用

C语言中getopt()函数的用法

学习后，下面是我写的测试程序来试验一下，

#include <stdio.h>
#include <getopt.h>
#include <stdlib.h>
#include <unistd.h>

extern char* optarg;
extern int optind, opterr, optopt;

int main(int argc, char *argv[]) {
    char op;
    while((op = getopt(argc, argv, "hvs:E:b:t:")) != EOF) {
        printf("optind = %d, op = %c\n", optind, op);
        switch(op) {
            case 'h':
                puts("option: -h"); break;
            case 'v':
                puts("option: -v"); break;
            case 's':
                printf("option: -s %s\n", optarg); break;
            case 'E':
                printf("option: -E %s\n", optarg); break;
            case 'b':
                printf("option: -b %s\n", optarg); break;
            case 't':
                printf("option: -t %s\n", optarg); break;
            default:
                printf("Unknown option: %c\n", optopt);
        }
    }
    return 0;
}

缓存模拟器其实并不难写，经过几次手动模拟测试数据，确保对缓存机制理解清楚后就可以上手了。一开始我看给的数据里面地址的位宽还不同，对 m = 64 还有点疑问，后来发现其实只要 s 和 b 定下来了，地址左边剩下的部分就是 tag 了，有多长并不需要知道。这里有两点 C 语言学到的新东西简单说下：

  1. 解析地址的时候 16 进制数为了避免判断字母是大写还是小写，可以使用 strtoull 函数，可以支持多种进制的转换，转换后就是 unsigned long long 类型（ atoi 不支持 16 进制）

  2. 高维数组的指针类型，像下面这样产生的指针就确实是指向二维数组的，而不是通过二级指针来分配高维数组：

    int (*cache)[E] = (int(*)[E])malloc(sizeof(int) * S * E);
int (*valid)[E] = (int(*)[E])malloc(sizeof(int) * S * E);

    传递参数：

    void cache_once(int (*cache)[E], int (*valid)[E], uint64 addr);

此外还需要理解到的是缓存模拟器中一次 L 和一次 S 产生的效果是一样的，而一次 M 相当于一次 L + 一次 S（等价于一次 L + 一次 hit）。

写完后 make 构建，

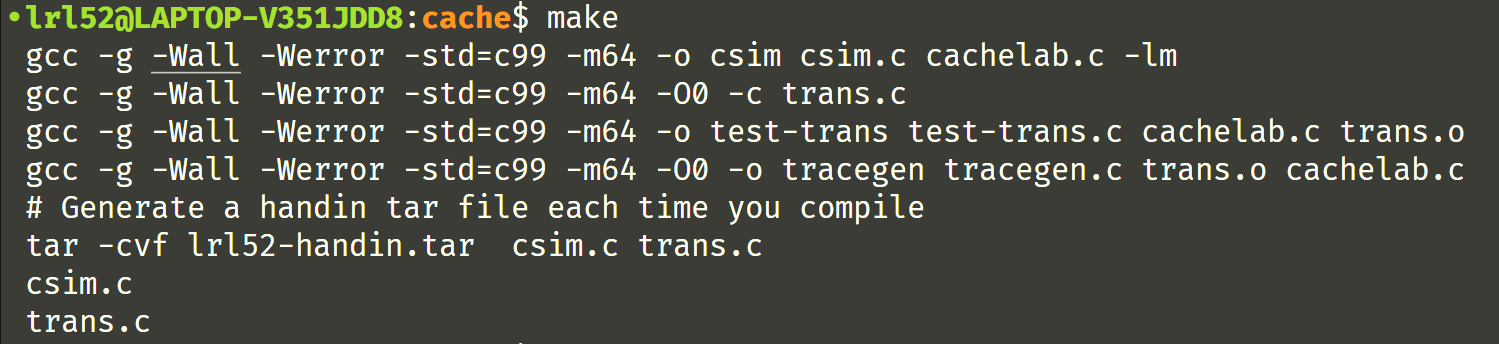
image-20230101231215607

测试一下，发现 -v 的输出有点小问题，

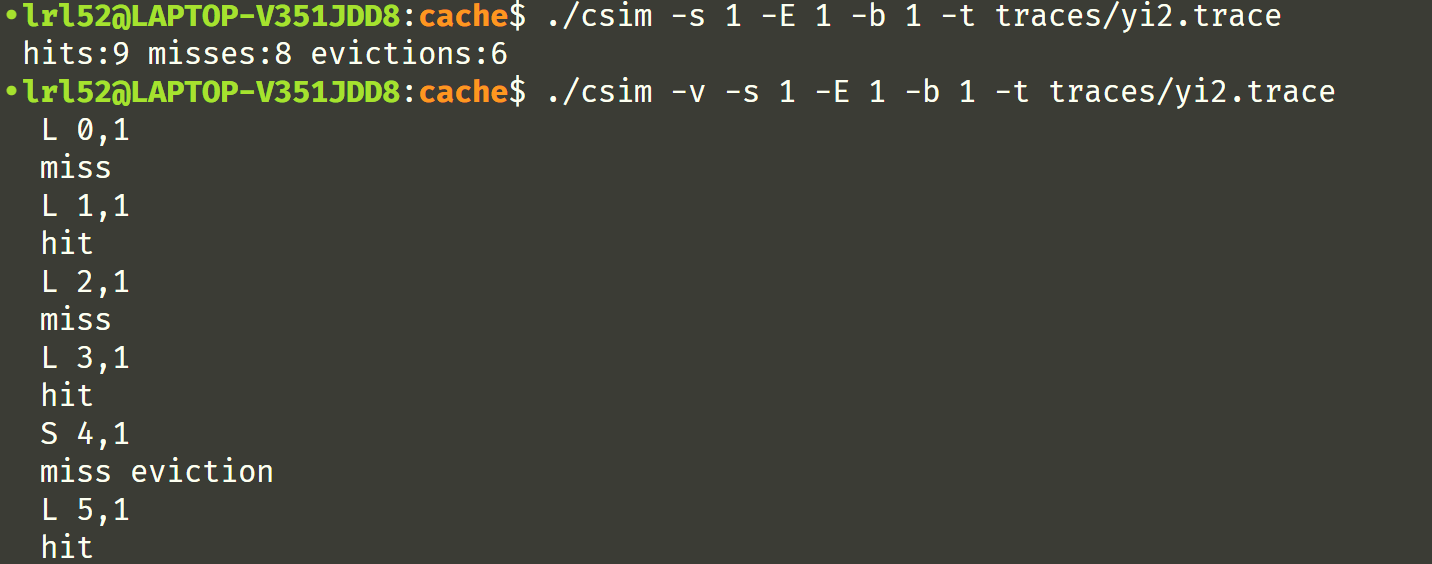
image-20230101231229662

调整一下，

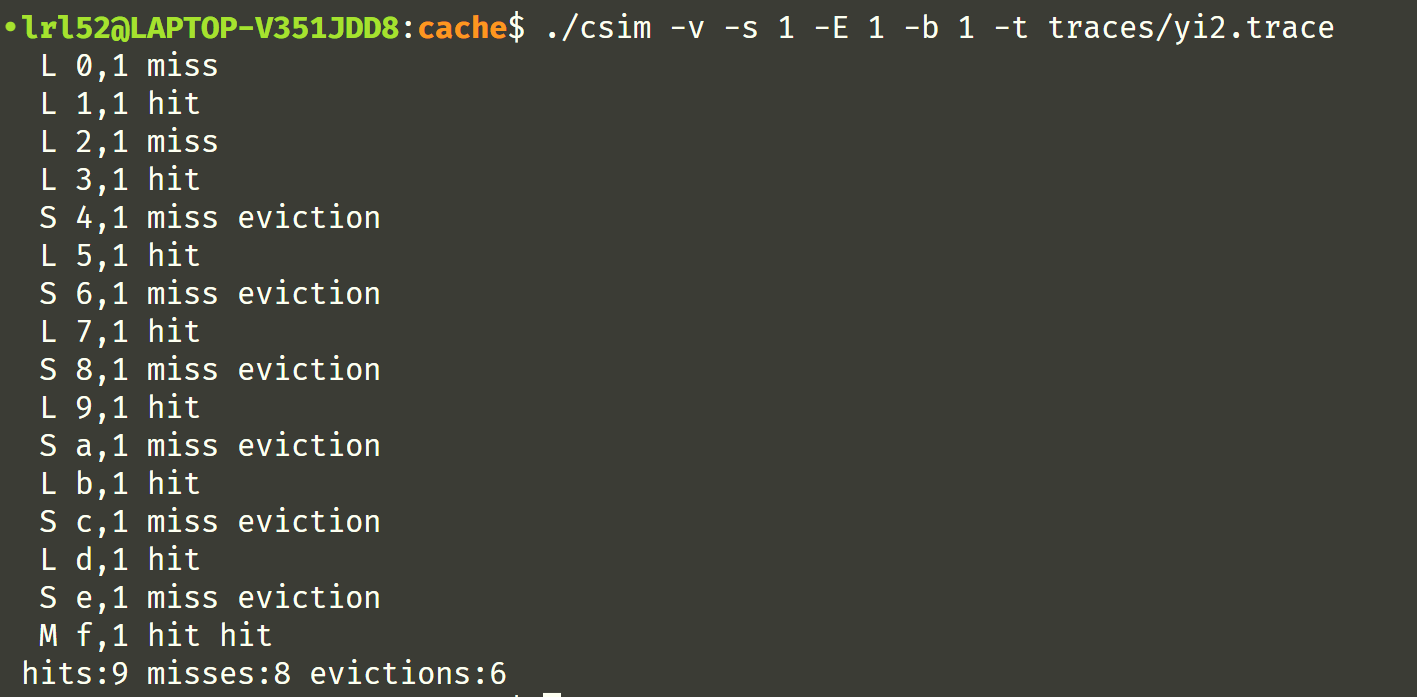
image-20230101231627522

完美，一次通过！

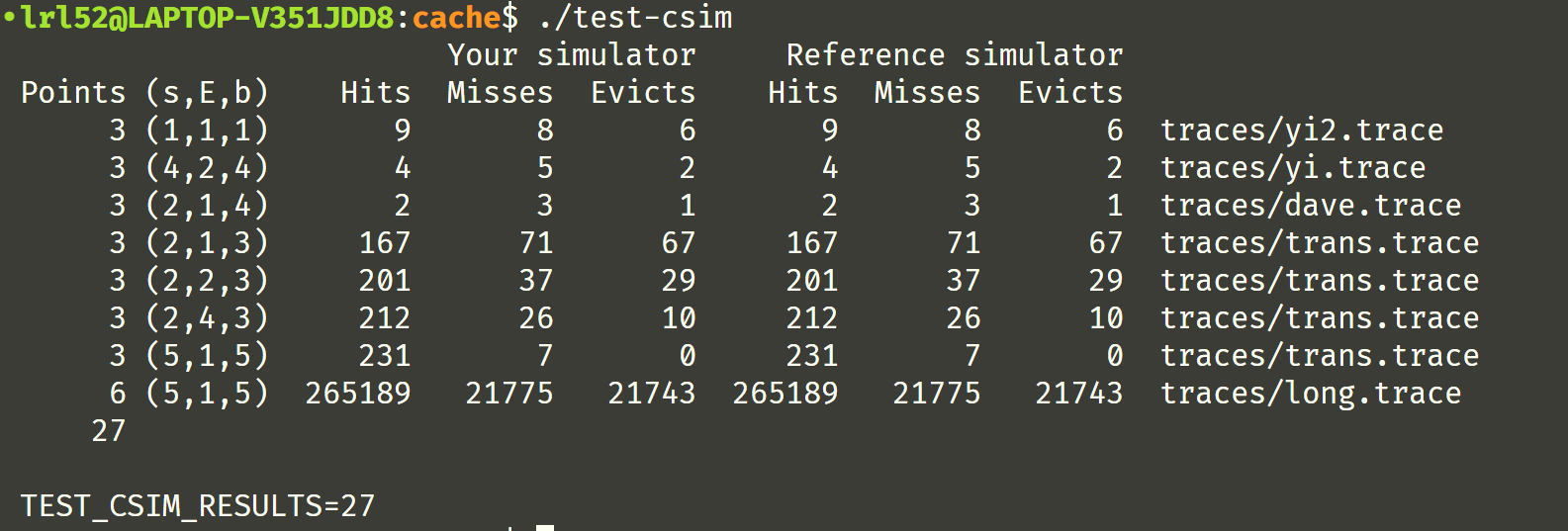
image-20230101232222286

完整代码如下：

#include <stdio.h>
#include <string.h>
#include <getopt.h>
#include <stdlib.h>
#include <unistd.h>
#include <assert.h>
#include "cachelab.h"

typedef unsigned long long uint64;

extern char* optarg;
extern int optind, opterr, optopt;

int debug_mode = 0;
int S, s, E, b, B; // 高速缓存的结构用元组 (S, E, B, m) 来描述，这里 m = 64
int hit_count = 0, miss_count = 0, eviction_count = 0;
#define MAXSIZE 105
char input[MAXSIZE];

static const char *helpinfo = "Usage: ./csim [-hv] -s <num> -E <num> -b <num> -t <file>\n" \
                 "Options:\n"
                 "  -h         Print this help message.\n" \
                 "  -v         Optional verbose flag.\n" \
                 "  -s <num>   Number of set index bits.\n" \
                 "  -E <num>   Number of lines per set.\n" \
                 "  -b <num>   Number of block offset bits.\n" \
                 "  -t <file>  Trace file.\n\n"
                 "Examples:\n" \
                 "  linux>  ./csim -s 4 -E 1 -b 4 -t traces/yi.trace\n" \
                 "  linux>  ./csim -v -s 8 -E 2 -b 4 -t traces/yi.trace\n";

uint64 read_addr(const char *str) { //确保格式是 [space]operation address,size
    uint64 ret = 0;
    char *end_p;
    ret = strtoull(str + 3, &end_p, 16);
    assert(end_p[0] == ',');
    return ret;
}

void debug(const char *str) {
    // if(debug_mode) printf("%s", str);
    if(debug_mode) {
        int len = strlen(str);
        for(int i = 0; i < len; ++i)
            if(i == 0 || str[i] != '\n')
                putchar(str[i]);
    }
}

void cache_once(int (*cache)[E], int (*valid)[E], uint64 addr) {
    static size_t cnt = 0;
    debug(input);
    uint64 mask = S - 1;
    uint64 group = (addr >> b) & mask, tag = addr >> (s + b);
    for(int i = 0; i < E; ++i) {
        if(valid[group][i] && cache[group][i] == tag) {
            ++hit_count;
            valid[group][i] = ++cnt;
            debug(" hit");
            return;
        }
    }
    ++miss_count;
    debug(" miss");
    size_t min_cnt = valid[group][0], sel = 0;
    for(int i = 1; i < E; ++i) {
        if(valid[group][i] < min_cnt) {
            min_cnt = valid[group][i];
            sel = i;
        }
    }
    if(min_cnt > 0) {
        ++eviction_count;
        debug(" eviction");
    }
    cache[group][sel] = tag;
    valid[group][sel] = ++cnt;
}

void cache_twice(int (*cache)[E], int (*valid)[E], uint64 addr) {
    cache_once(cache, valid, addr);
    ++hit_count;
    debug(" hit");
}

int main(int argc, char *argv[]) {
    char op;
    FILE *fp;
    while((op = getopt(argc, argv, "hvs:E:b:t:")) != EOF) {
        // printf("optind = %d, op = %c\n", optind, op);
        switch(op) {
            case 'h':
                // puts("option: -h");
                printf("%s", helpinfo);
                return 0;
            case 'v':
                // puts("option: -v");
                debug_mode = 1; break;
            case 's':
                // printf("option: -s %s\n", optarg);
                s = atoi(optarg); break;
            case 'E':
                // printf("option: -E %s\n", optarg);
                E = atoi(optarg); break;
            case 'b':
                // printf("option: -b %s\n", optarg);
                b = atoi(optarg); break;               
            case 't':
                // printf("option: -t %s\n", optarg);
                fp = fopen(optarg, "r");
                if(!fp) {
                    printf("Error: fail to open %s\n", optarg);
                    exit(EXIT_FAILURE);
                }  
                break;
            default:
                printf("Unknown option: %c\n", optopt);
        }
    }
    S = 1 << s, B = 1 << b;
    // cache 数组代表高速缓存，存的是 tag 字段，记录缓存被谁占用了
    int (*cache)[E] = (int(*)[E])malloc(sizeof(int) * S * E);
    // valid 数组代表合法性，非0表示有效，数值大小即最后一次访问的时间戳，用于 LRU 替换时的比较值
    int (*valid)[E] = (int(*)[E])malloc(sizeof(int) * S * E);
    if(!cache || !valid) {
        puts("Error: run out of memory!");
        exit(EXIT_FAILURE);
    }
    for(int i = 0; i < S; ++i)
        for(int j = 0; j < E; ++j)
            cache[i][j] = valid[i][j] = 0;
    uint64 addr;
    while(fgets(input, MAXSIZE, fp)) {
        if(input[0] == 'I') continue;
        assert(input[0] == ' ');
        assert(input[1] == 'L' || input[1] == 'S' || input[1] == 'M');
        addr = read_addr(input);
        if(input[1] == 'L' || input[1] == 'S') cache_once(cache, valid, addr);
        else cache_twice(cache, valid, addr);
        debug("\n");
    }
    free(cache);
    free(valid);
    printSummary(hit_count, miss_count, eviction_count);
    return 0;
}

Google search for cache 的时候发现的“一生一芯”，stO 孟爷爷

Part B：矩阵转置优化

Part A 大概只算开胃菜，没什么难度。 Part B 才是有意思、有挑战难度的任务?。

Part B 任务如题，具体要求见文档，总共有 3 个子任务。

先试试水，看看没有优化的转置函数默认 run 后测试的结果，貌似 Simple row-wise scan transpose 的数据和文档上有点小不同

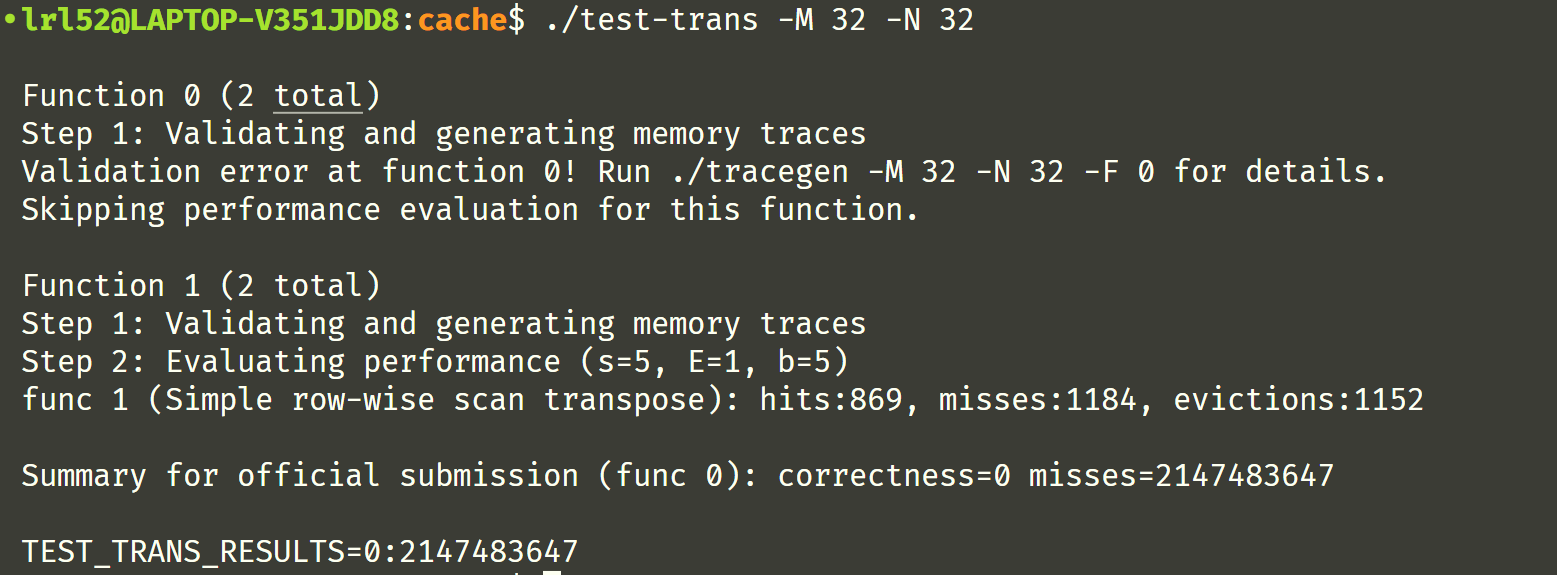
image-20230103163628649

哈哈，因为 misses 数量超出了最高限制，直接 0 分。是不是感觉这个测试风格似曾相识，在 Performance Lab 中我们做过矩阵的 rotate 优化，rotate 包含了转置这一步，这不直接拿来改改用用，当时写的是 8x8 分块矩阵优化：

char transpose_submit_desc[] = "Transpose submission";
void transpose_submit(int M, int N, int A[N][M], int B[M][N]) {
    const int up1 = M - 7, up2 = N - 7;
    register int i, j, k;
    for(i = 0; i < up1; i += 8) {
        for(j = 0; j < up2; j += 8) {
            for(k = i; k < i + 8; ++k) {
                B[j + 0][k] = A[k][j + 0];
                B[j + 1][k] = A[k][j + 1];
                B[j + 2][k] = A[k][j + 2];
                B[j + 3][k] = A[k][j + 3];
                B[j + 4][k] = A[k][j + 4];
                B[j + 5][k] = A[k][j + 5];
                B[j + 6][k] = A[k][j + 6];
                B[j + 7][k] = A[k][j + 7];
            }
        }
        for( ; j < N; ++j) {
            B[j][i + 0] = A[i + 0][j];
            B[j][i + 1] = A[i + 1][j];
            B[j][i + 2] = A[i + 2][j];
            B[j][i + 3] = A[i + 3][j];
            B[j][i + 4] = A[i + 4][j];
            B[j][i + 5] = A[i + 5][j];
            B[j][i + 6] = A[i + 6][j];
            B[j][i + 7] = A[i + 7][j];
        }
    }
    for( ; i < M; ++i) {
        for(j = 0; j < up2; j += 8) {
            B[j + 0][k] = A[k][j + 0];
            B[j + 1][k] = A[k][j + 1];
            B[j + 2][k] = A[k][j + 2];
            B[j + 3][k] = A[k][j + 3];
            B[j + 4][k] = A[k][j + 4];
            B[j + 5][k] = A[k][j + 5];
            B[j + 6][k] = A[k][j + 6];
            B[j + 7][k] = A[k][j + 7];
        }
        for( ; j < N; ++j)
            B[j][i] = A[i][j];
    }
}

可惜没有低于 300，没有拿到全部分数

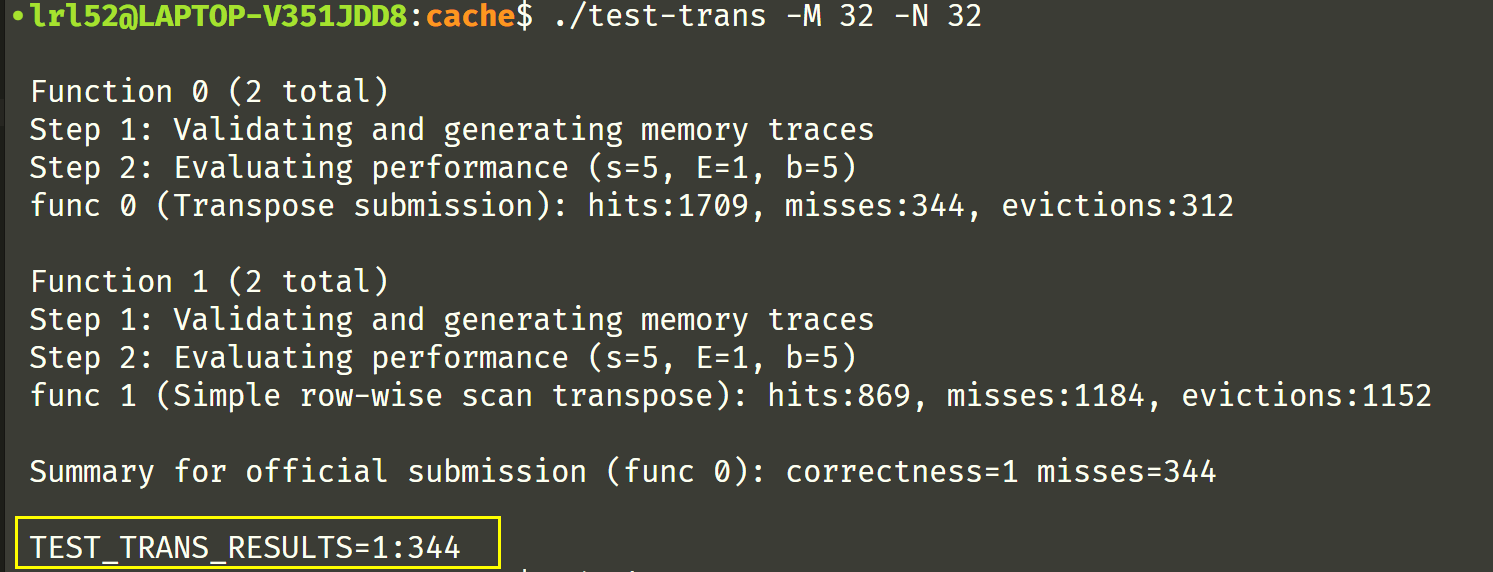
image-20230103170424036

来试试用给的 py 脚本测测总分数

python2 ./driver.py

跑得很慢，估计是那个 valgrind trace 的时候太浪费时间了

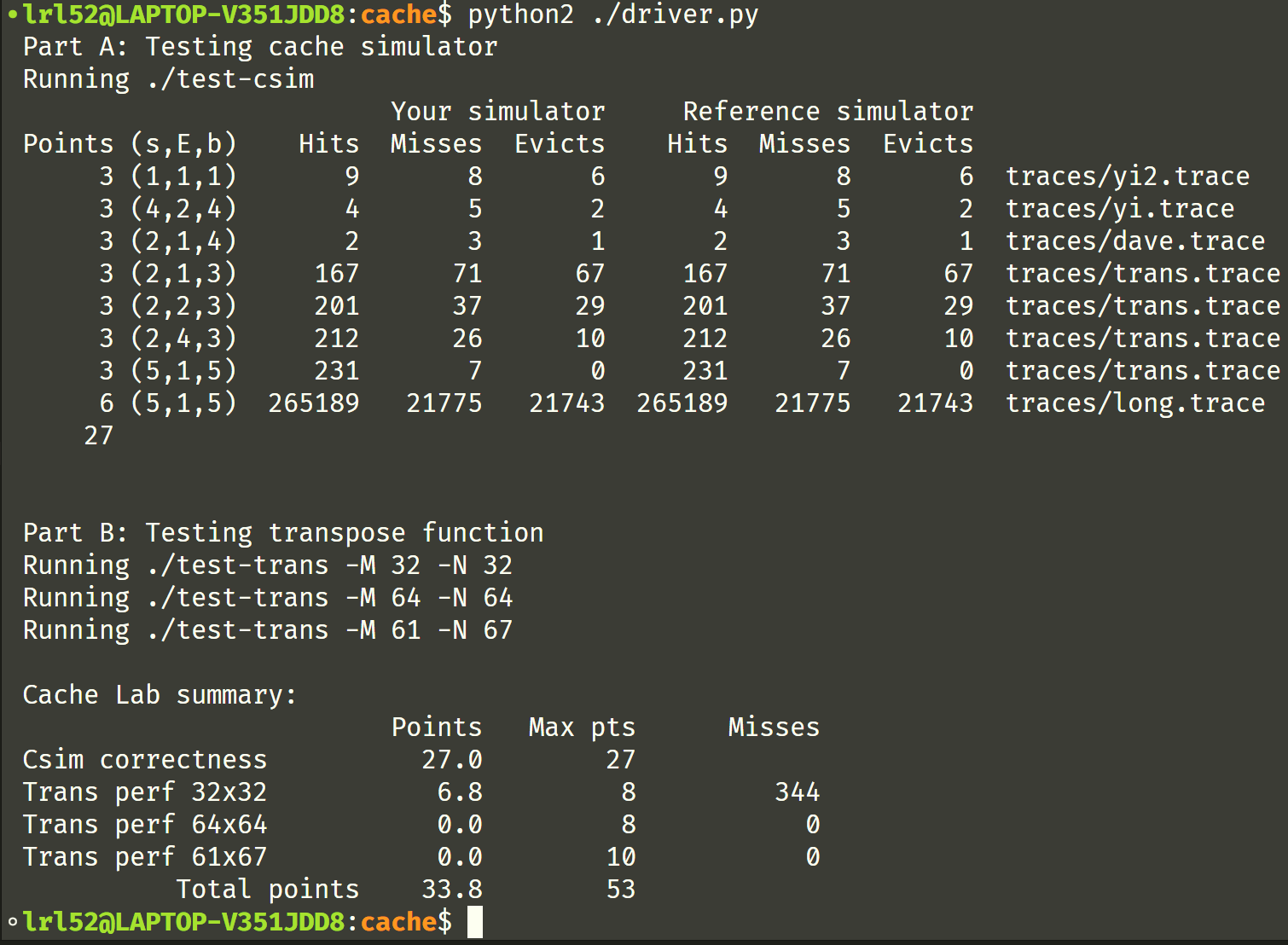
跑了好几分钟，原来转置后面 2 个数据是 0 分啊?

image-20230103171630001

Task 1：32 x 32

参考了网上的做法，正解就是 8x8 分块。为什么呢？因为 s = b = 5, E = 1，采用直接映射法，每个 block 的大小是 $2^5 = 32$ 字节，恰好能装 8 个 int，共有 32 组，缓存大小是 1024 Bytes。8x8 矩阵的每一行恰能装入一个 set，因此采用 8x8 的分块矩阵能够最大限度的利用缓存，内存映射示意图如下，

img

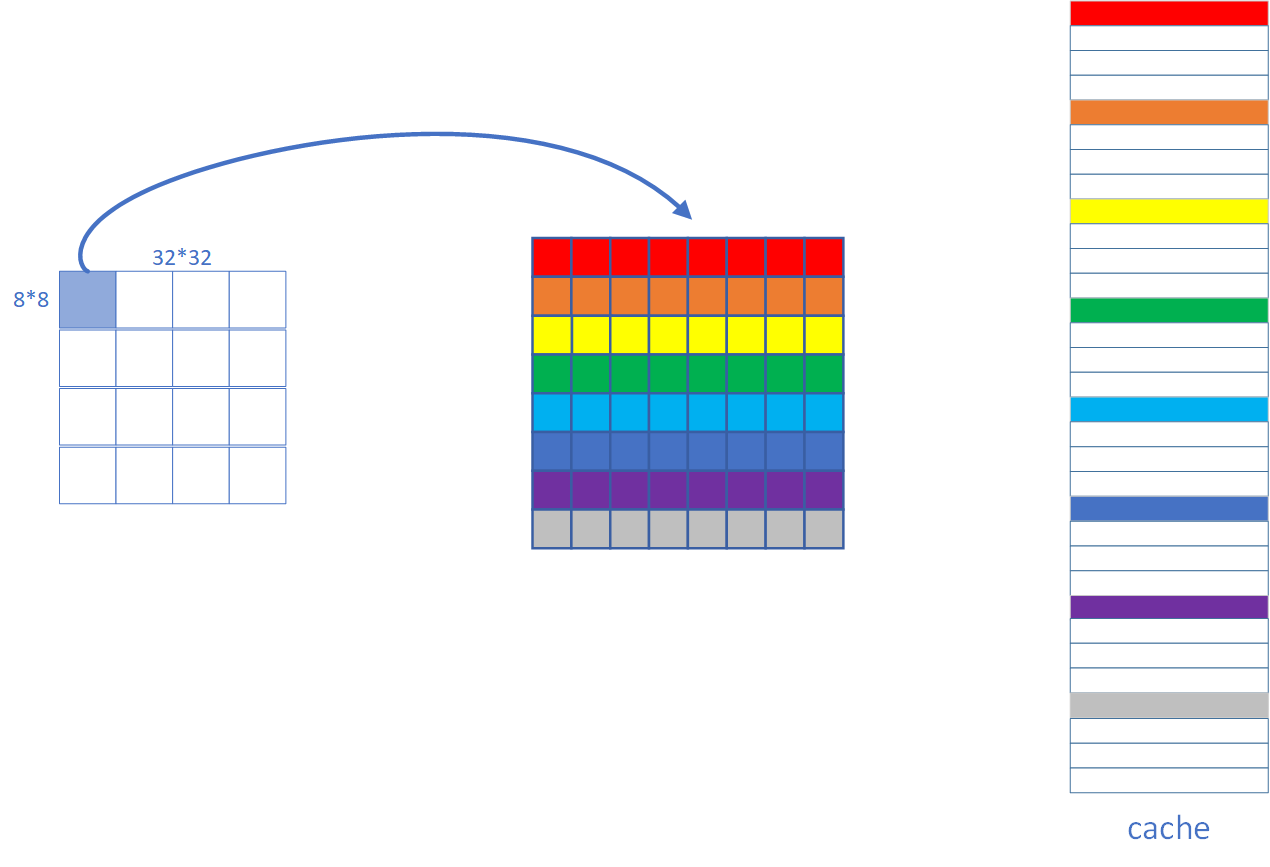
由于本题的 N, M 是已经固定了，可以仅仅针对这 3 组数据来优化，所以原来循环展开多余的部分就可以不要了，改了后如下，

char transpose_submit_desc[] = "Transpose submission";
void transpose_submit(int M, int N, int A[N][M], int B[M][N]) {
    register int i, j, k;
    for(i = 0; i < M; i += 8) {
        for(j = 0; j < N; j += 8) {
            for(k = i; k < i + 8; ++k) {
                B[j + 0][k] = A[k][j + 0];
                B[j + 1][k] = A[k][j + 1];
                B[j + 2][k] = A[k][j + 2];
                B[j + 3][k] = A[k][j + 3];
                B[j + 4][k] = A[k][j + 4];
                B[j + 5][k] = A[k][j + 5];
                B[j + 6][k] = A[k][j + 6];
                B[j + 7][k] = A[k][j + 7];
            }
        }
    }
}

可惜得到的结果依然是 344，没有拿到满分，为什么呢？因为 conflict misses （具体见后文）

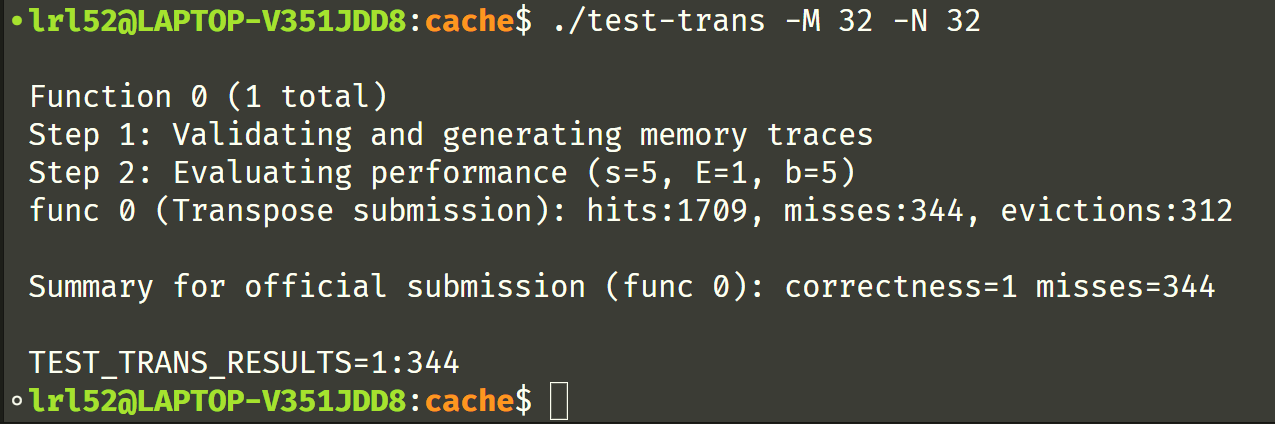
image-20230103220746603

因为理论上的 misses 应该为 $4 \times 32 \times 2 = 256$，为了减少对角线冲突，可以利用局部变量，总共可以定义 12 个局部变量，4 个作为循环变量，另外 8 个就可以作为临时变量，连续读矩阵，从而减少在对角线附近的缓存冲突，

char transpose_submit_desc[] = "Transpose submission";
void transpose_submit(int M, int N, int A[N][M], int B[M][N]) {
    register int i, j, k;
    int t0, t1, t2, t3, t4, t5, t6, t7;
    for(i = 0; i < M; i += 8) {
        for(j = 0; j < N; j += 8) {
            for(k = i; k < i + 8; ++k) {
                t0 = A[k][j + 0], t1 = A[k][j + 1];
                t2 = A[k][j + 2], t3 = A[k][j + 3];
                t4 = A[k][j + 4], t5 = A[k][j + 5];
                t6 = A[k][j + 6], t7 = A[k][j + 7];
                B[j + 0][k] = t0, B[j + 1][k] = t1;
                B[j + 2][k] = t2, B[j + 3][k] = t3;
                B[j + 4][k] = t4, B[j + 5][k] = t5;
                B[j + 6][k] = t6, B[j + 7][k] = t7;
            }
        }
    }
}

wow，第一个终于过了

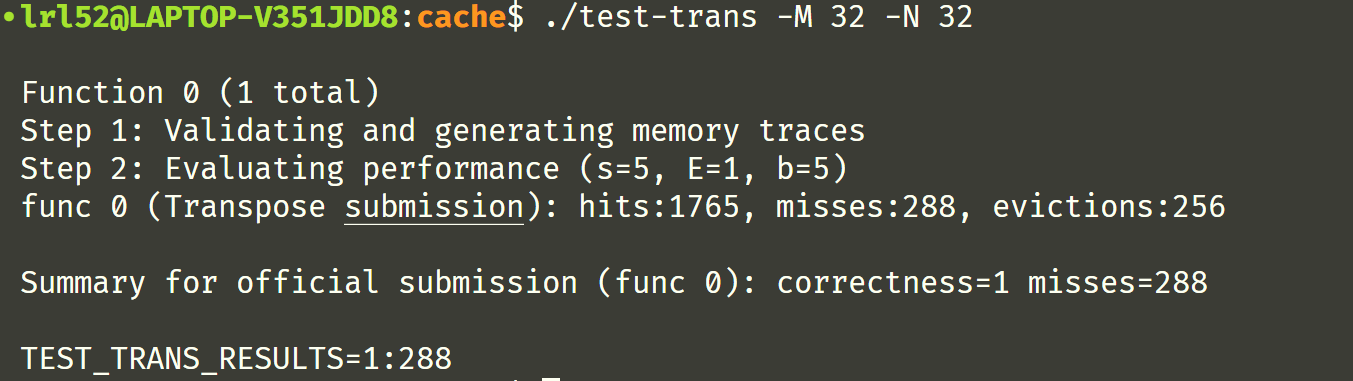
image-20230103221308415

关于对角线冲突的分析

即 conflict miss ，尤其是在对角线上，A 和 B 矩阵会发生缓存使用冲突，关于这点，就需要详细了解下具体的缓存分布情况了，PPT 上有这么一句话：

image-20230104203723540

需要理解到的是两个矩阵的任意相同位置（x, y）所属的 set 是相同的，在对角线上的时候，由于转置后位置不变，所以 A 和 B 矩阵会发生 conflict miss。这是为什么呢？第一天的时候有 blog 这么说也困扰着我，第二天我亲自去看测试源码 A 和 B 矩阵的生成，发现矩阵并不是通过两次 malloc 分配的，而是编译就确定好的，

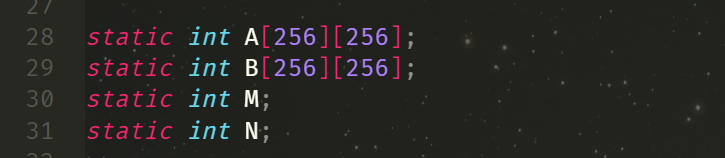
image-20230104204300209

这样就好说了，可以猜到 A 和 B 的内存是地址是连续的，可以简单验证一下：

#include <stdio.h>

static int A[256][256];
static int B[256][256];


int main() {
    unsigned long long a1 = A, a2 = B;
    printf("%llu %llu\n", &A[255][255], B);
    printf("%llu %llu\n", a1, a2);
    printf("%lld %llu\n", a1 / 32 % 32, a2 / 32 % 32);
    return 0;
}

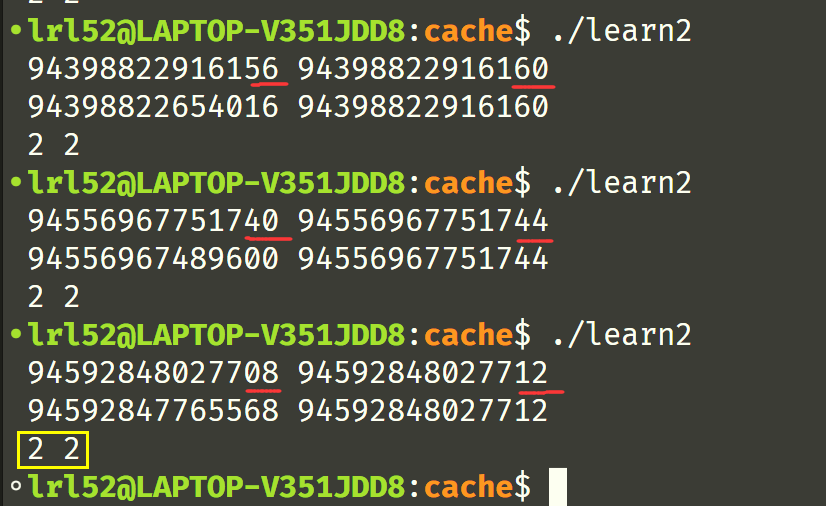
果真，内存地址连续， 首地址分配到 cache 的 set 相同，因此两个矩阵的任意相同位置（x, y）所属的 set 是相同的

image-20230104144603437

Task 2：64 x 64

这部分算上整个 cache lab 的压轴部分吧，也是最难的部分，很多 blog 上的文章都放弃了。然而作者码字好累啊。

这一部分如果直接按 Task 1 的方法 8x8 分块是不行的，因为这下一个 8x8 的块是不能完全装入 cache 的，第 1 行会与第 5 行冲突，具体图如下：

img

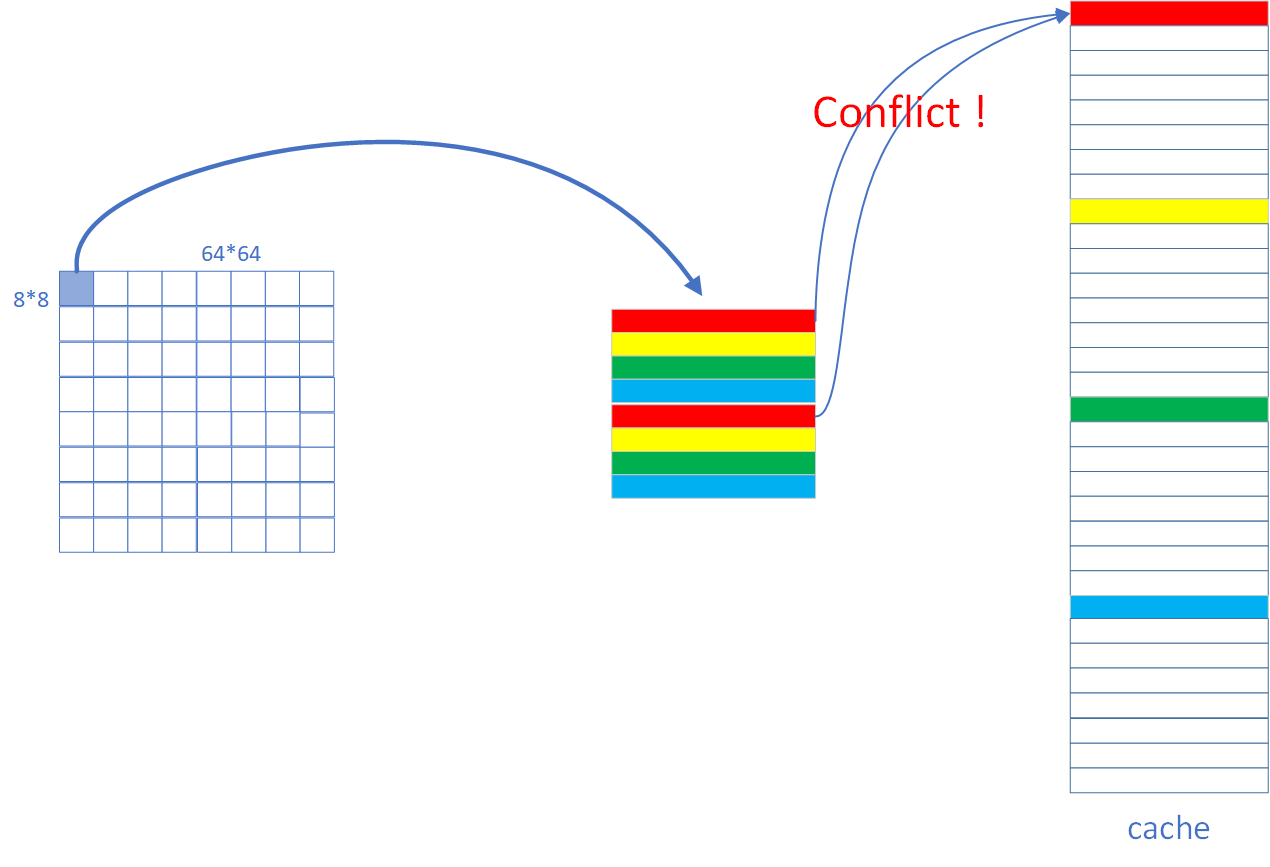
如果按照 4x4 分块，会无法分利用到缓存，最后大概 1699 次 misses，不能拿到满分。因此最终方案还是需要 8x8 分块，但会有很强的 trick 。

先上一张 64x64 的完整缓存分布图如下：

img

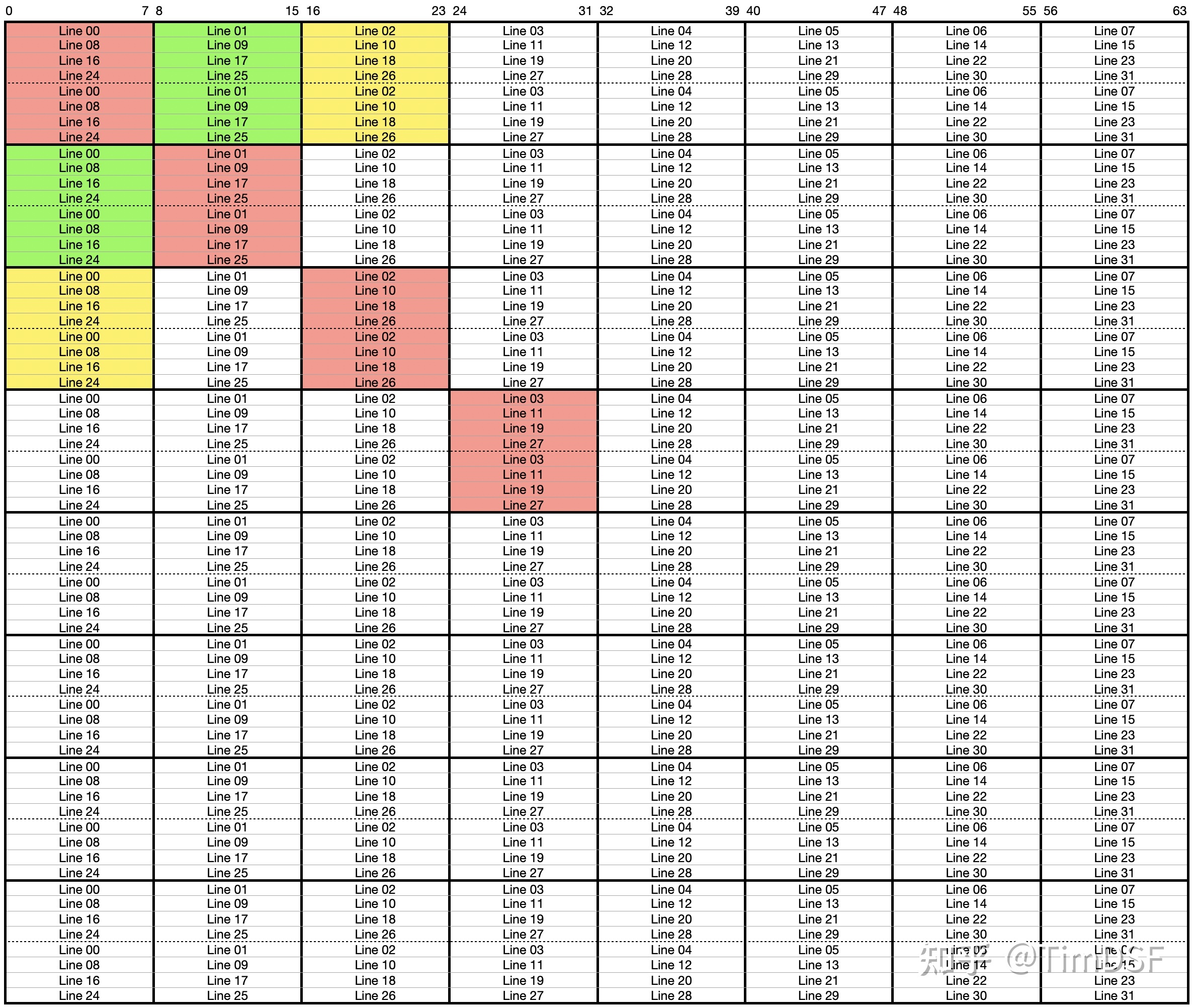
这部分我找了好几个 blog，最终这个写得还不戳，图比较多，稍微容易理解一点。我在看了 blog 后总结出了一份完整的流程图，需要在 8x8 的分块矩阵里继续按照 4x4 分块：

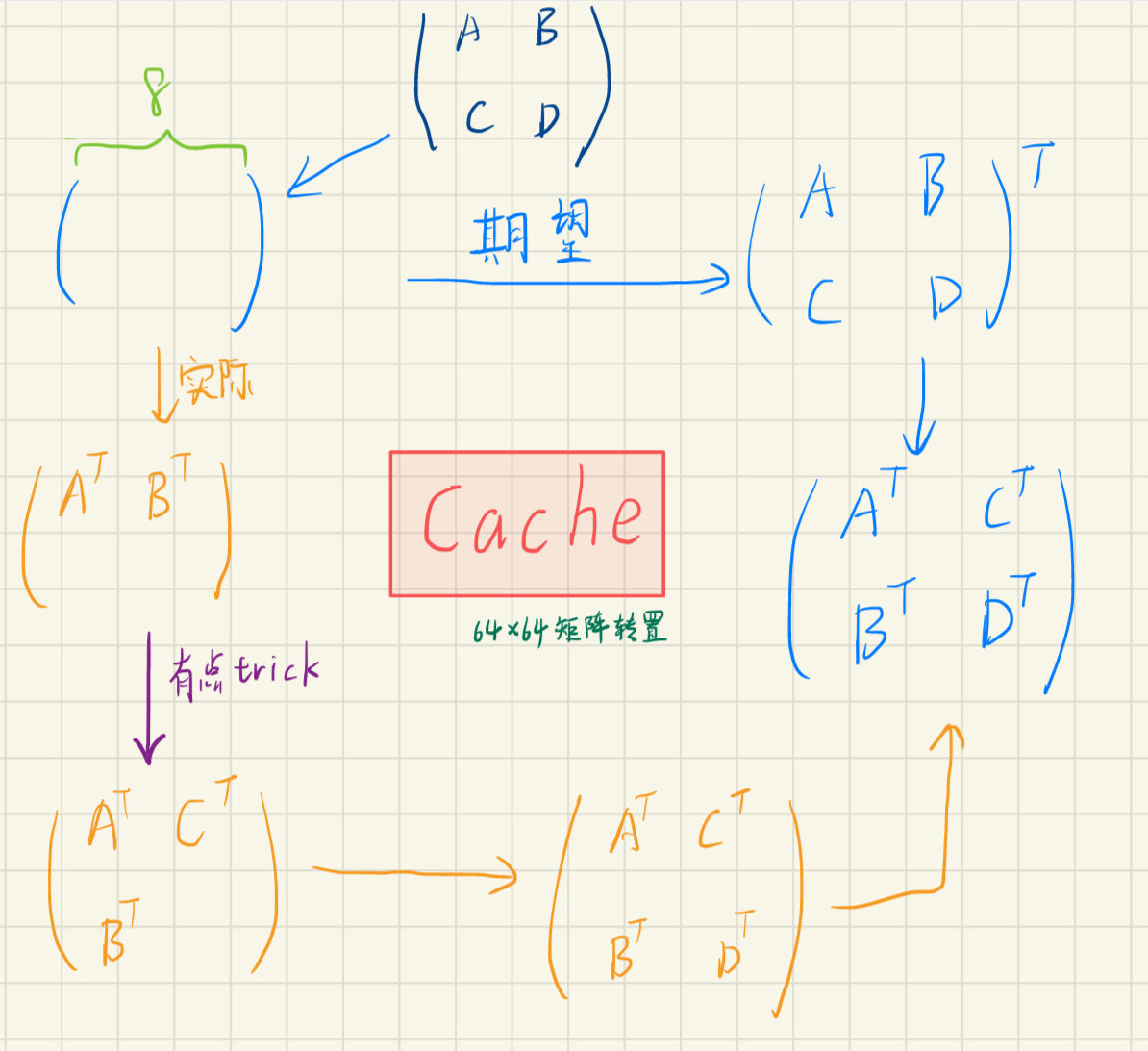
image-20230104210617612

在理解这份整个流程和细节后，就可以写代码了。总而言之，就是在写目标 B 矩阵的时候只能连续 4 行写完再继续写，因此一开始分块矩阵 $B^T$ 没有放置在正确的位置上，之后需要在放置 $C^T$ 的同时把 $B^T$ 挪到正确的位置上，这一步很关键也有比较强的 trick，自己动脑想想吧。最后把 $D^T$ 移过去就完成了一次 8x8 分块的转置过程。（注意分清文章中的 $B$ 是 4x4 的小分块矩阵还是大矩阵 ?）

misses 的理论下限值是 $ 8 \times 64 \times 2 = 1024$

好，写完了，测试一下，

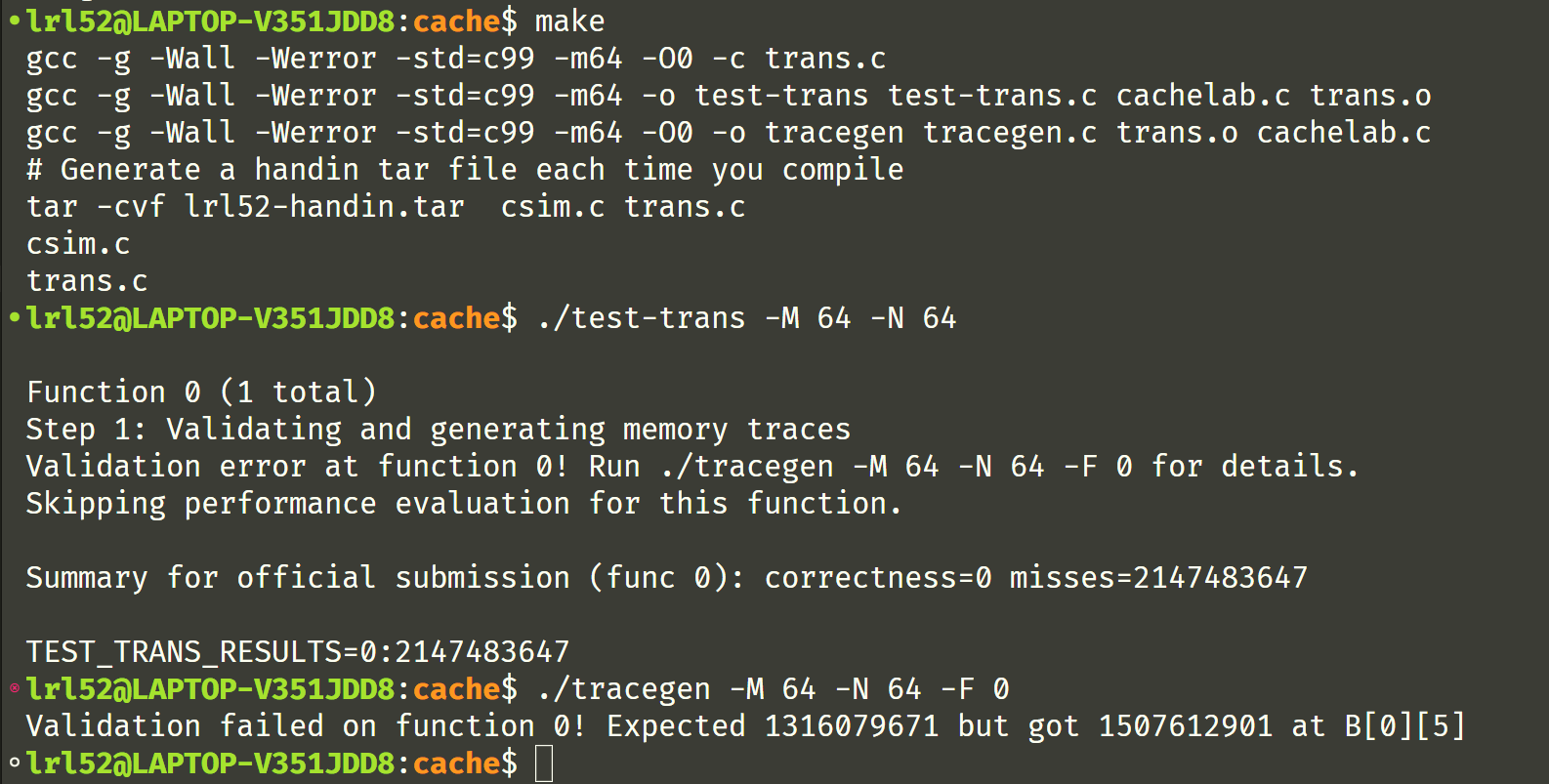
image-20230104170742584

经过不懈努力和更改，转置算法终于正确了，拿到了 misses=1180 的成绩，满分了！

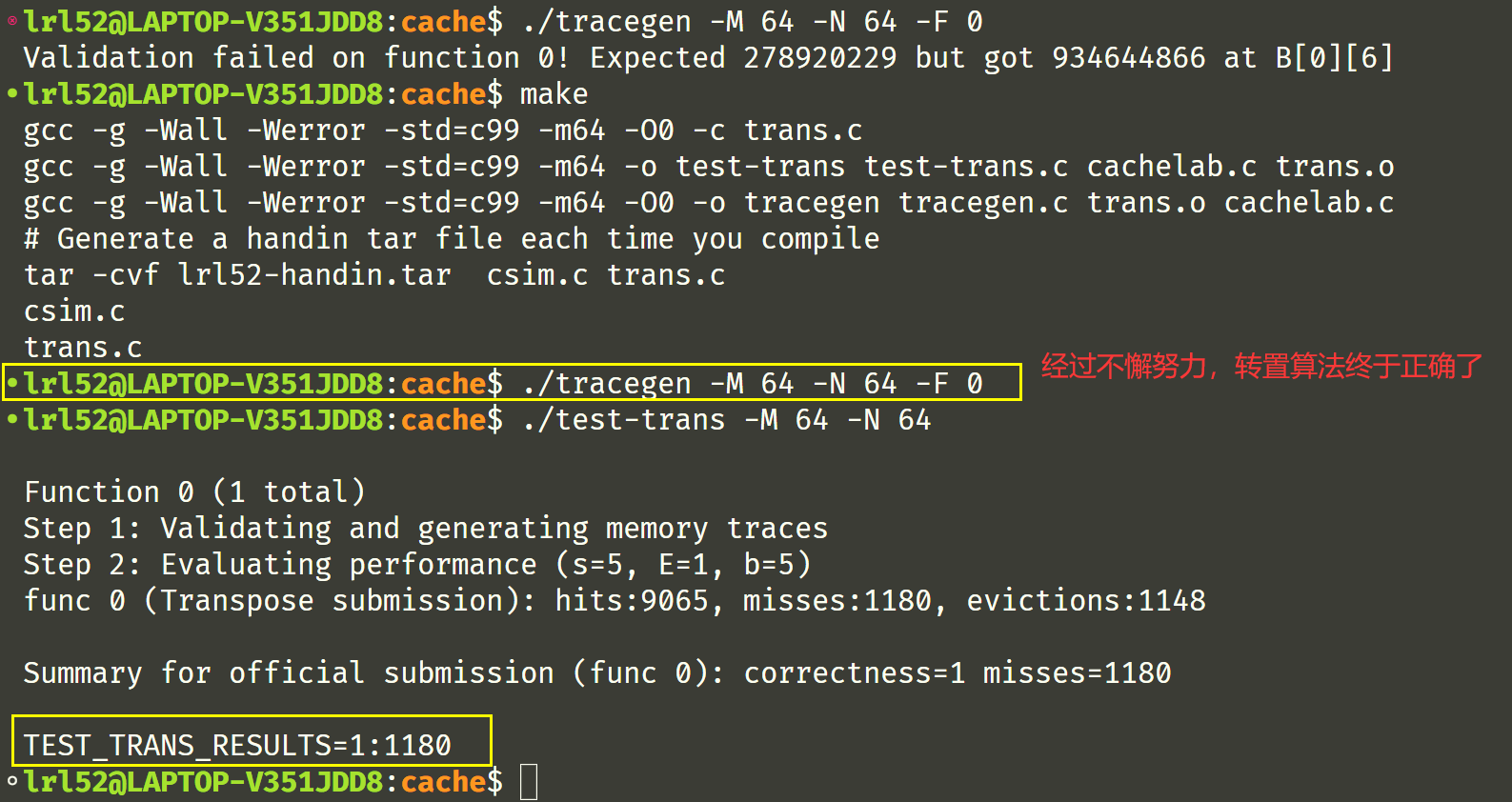
image-20230104172355907

完整代码在 Task 3 放出。

Task 3：61 x 67

这个部分其实比较简单了，由于大小不规则，只能不断尝试分块矩阵的大小，网上找到一个表格如下：

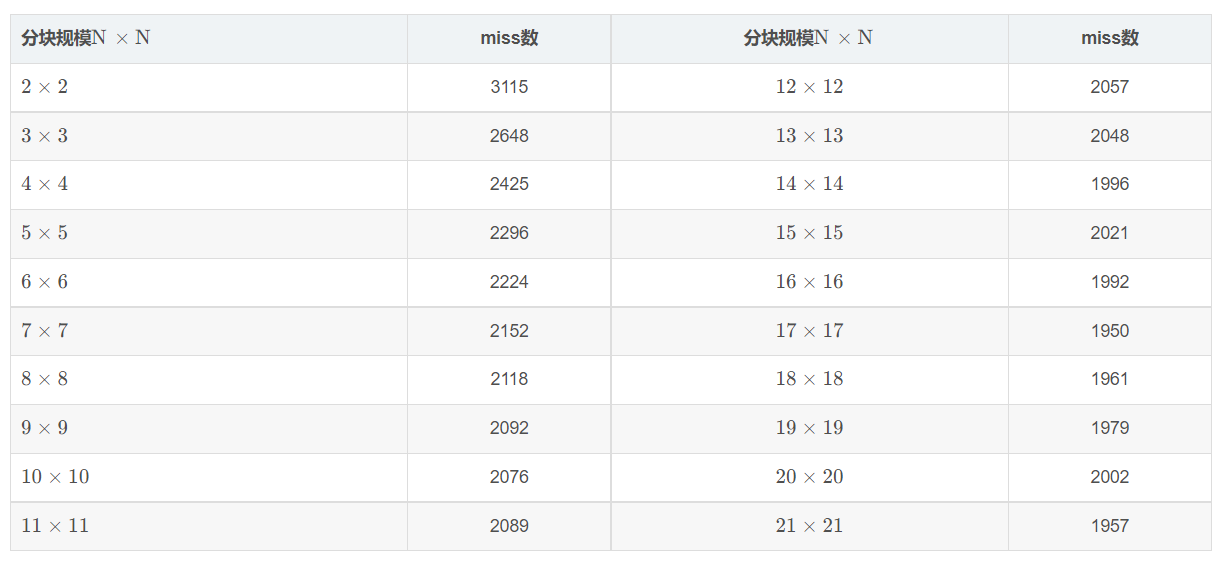
image-20230104212333077
block 大小为 16 时的结果：

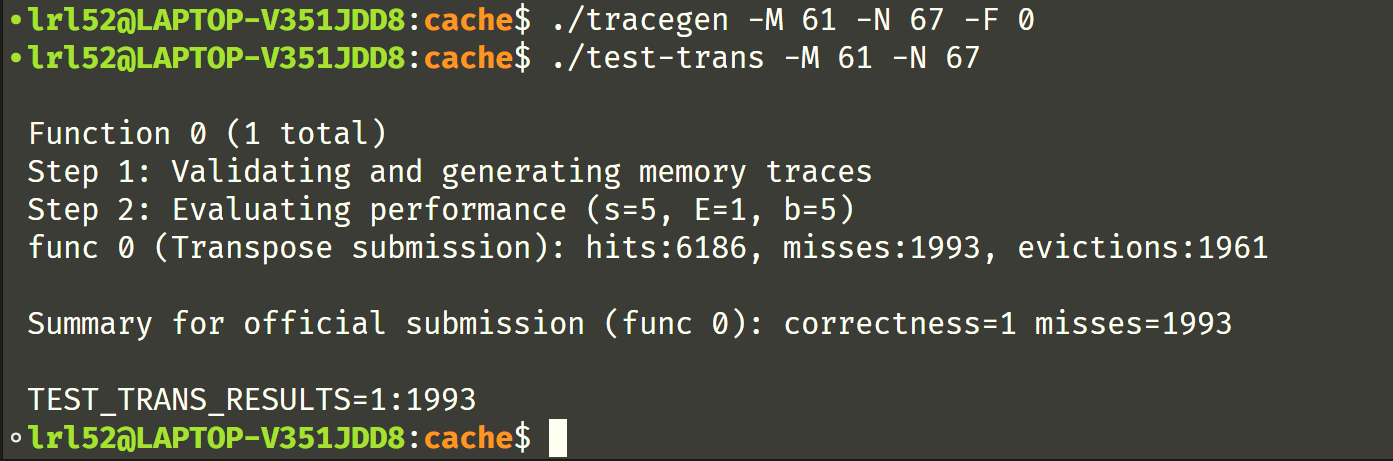
image-20230104174106578

block 大小为 17 时的结果：

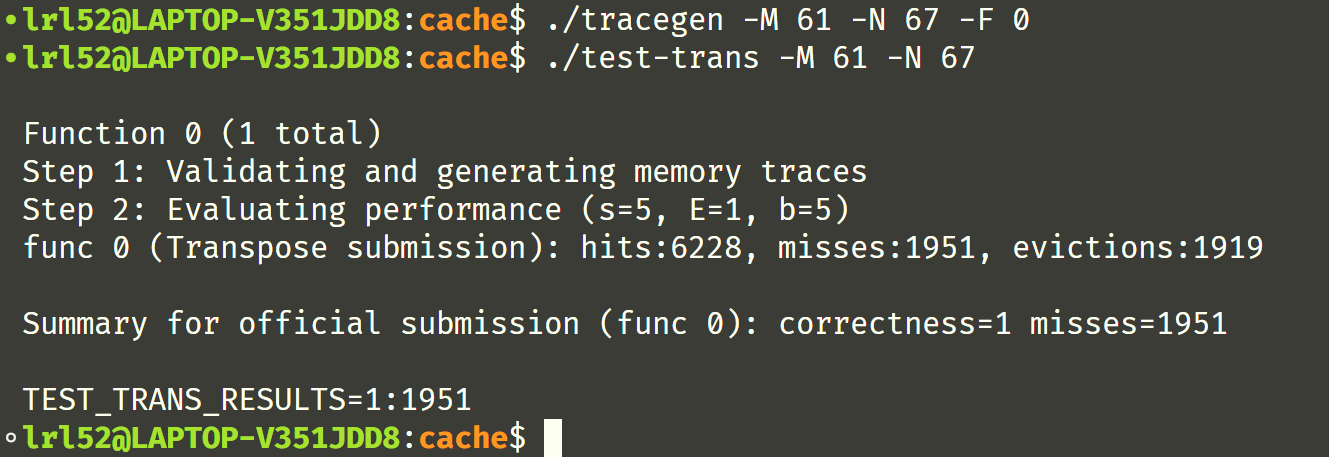
image-20230104174402521

因此采用 17x17 的分块，Part B 的完整代码如下：

char transpose_submit_desc[] = "Transpose submission";
void transpose_submit(int M, int N, int A[N][M], int B[M][N]) {
    register int i, j, k, h;
    int t0, t1, t2, t3, t4, t5, t6, t7;
    if(M == 32 && N == 32) {
        for(i = 0; i < M; i += 8) {
            for(j = 0; j < N; j += 8) {
                for(k = i; k < i + 8; ++k) {
                    t0 = A[k][j + 0], t1 = A[k][j + 1];
                    t2 = A[k][j + 2], t3 = A[k][j + 3];
                    t4 = A[k][j + 4], t5 = A[k][j + 5];
                    t6 = A[k][j + 6], t7 = A[k][j + 7];
                    B[j + 0][k] = t0, B[j + 1][k] = t1;
                    B[j + 2][k] = t2, B[j + 3][k] = t3;
                    B[j + 4][k] = t4, B[j + 5][k] = t5;
                    B[j + 6][k] = t6, B[j + 7][k] = t7;
                }
            }
        }
    } else
    if(M == 64 && N == 64) {
        for(i = 0; i < M; i += 8) {
            for(j = 0; j < N; j += 8) {
                for(k = i; k < i + 4; ++k) {
                    t0 = A[k][j + 0], t1 = A[k][j + 1];
                    t2 = A[k][j + 2], t3 = A[k][j + 3];
                    t4 = A[k][j + 4], t5 = A[k][j + 5];
                    t6 = A[k][j + 6], t7 = A[k][j + 7];
                    B[j + 0][k] = t0, B[j + 1][k] = t1;
                    B[j + 2][k] = t2, B[j + 3][k] = t3;
                    B[j + 0][k + 4] = t4, B[j + 1][k + 4] = t5;
                    B[j + 2][k + 4] = t6, B[j + 3][k + 4] = t7;
                }
                for(k = j, h = 0; h < 4; ++k, ++h) {
                    //取分块矩阵C里面的一列（注意：不是取一行，取一列才能让转置后变成一行）
                    t0 = A[i + 4][k], t1 = A[i + 5][k];
                    t2 = A[i + 6][k], t3 = A[i + 7][k];
                    //取分块矩阵B^T里面的一行
                    t4 = B[j + h][i + 4], t5 = B[j + h][i + 5];
                    t6 = B[j + h][i + 6], t7 = B[j + h][i + 7];
                    //先把分块矩阵C移到C^T的位置
                    B[j + h][i + 4] = t0, B[j + h][i + 5] = t1;
                    B[j + h][i + 6] = t2, B[j + h][i + 7] = t3;
                    //再把分块矩阵B^T移到正确的位置
                    B[j + h + 4][i + 0] = t4, B[j + h + 4][i + 1] = t5;
                    B[j + h + 4][i + 2] = t6, B[j + h + 4][i + 3] = t7;
                }
                for(k = i + 4; k < i + 8; ++k) {
                    t4 = A[k][j + 4], t5 = A[k][j + 5];
                    t6 = A[k][j + 6], t7 = A[k][j + 7];
                    B[j + 4][k] = t4, B[j + 5][k] = t5;
                    B[j + 6][k] = t6, B[j + 7][k] = t7;
                }
            }
        }
    } else 
    if(M == 61 && N == 67) {
        for(i = 0; i < N; i += 17) {
            for(j = 0; j < M; j += 17) {
                for(k = i; k < i + 17 && k < N; ++k) {
                    for(h = j; h < j + 17 && h < M; ++h) {
                        B[h][k] = A[k][h];
                    }
                }
            }
        }
    }
}

总结

最终运行测试脚本， cache lab 拿到了满分：

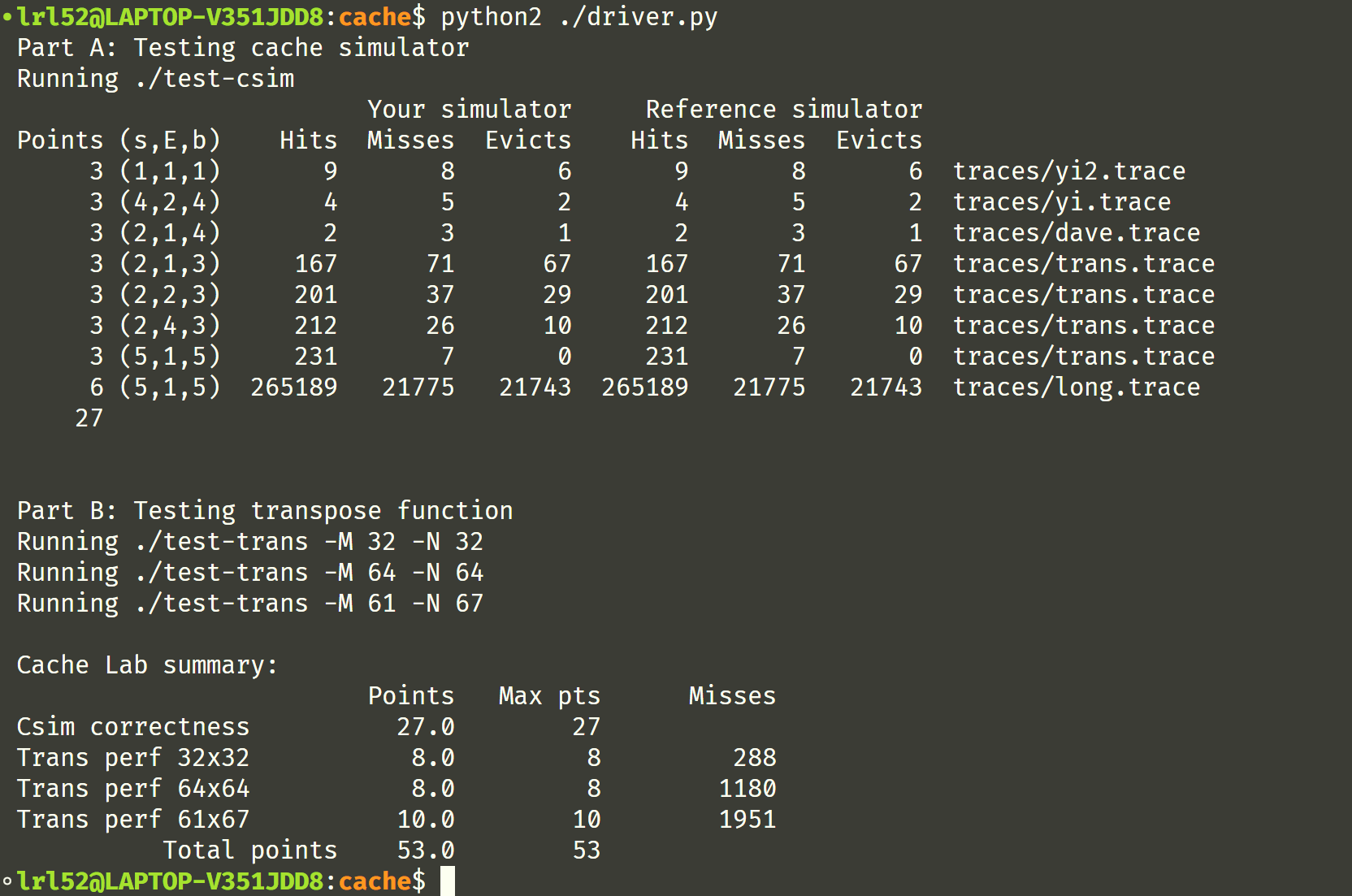
image-20230104175108727

前文写了这么多，总结也没有太多好说的了，cache lab 果真不负所望，相比之前的 performace lab 质量高多了。Part A 手写缓存模拟器让我深刻知道了缓存的运行机制，Part B 的缓存优化也很有意思，用分块（block）技术实现优化，这还运用到了线性代数分块矩阵的运算性质（其实这块学校课上也没有证明），尤其是 64x64 的部分有一定思维难度，相当具有挑战性。在做 Part B 的时候还读了一篇小论文，上面介绍了使用分块来加速矩阵乘法的实现。

Reference

CSDN：CSAPP(CMU 15-213)：Lab4 Cachelab详解（这个 64x64 部分讲的不戳）

CSDN：深入理解计算机系统-cachelab （上面那篇的博主就看的这篇，64x64 部分讲的不戳）

知乎：CSAPP – Cache Lab的更(最)优秀的解法（64x64 部分的神仙完美解法，卷到了理论下限值 1024，博主本人也卷到了 Lab 的 Rank 1）

知乎：CSAPP实验之cache lab

知乎：马天猫Masn的Cache Lab笔记

知乎：Cache的基本原理

CMU 官方视频地址

15-213/18-213/15-513: Intro to Computer Systems (ICS)

所有 Lab 的 PPT 地址

CSAPP
暂无评论

发送评论 编辑评论 


				

			

						

				

					

						

							

								
							

							
						

					

				

				

					

						

							

								
							

							
						

					

				

				

					

						

							

								
							

							
							
													

					

				

			

			
			

				

					
				

			

				

											

							
							
						

																

							
							
						

																

							
							
						

										
					
											
						

	

		
|´・ω・)ノ
ヾ(≧∇≦*)ゝ
(☆ω☆)
（╯‵□′）╯︵┴─┴
￣﹃￣
(/ω＼)
∠( ᐛ 」∠)＿
(๑•̀ㅁ•́ฅ)
→_→
୧(๑•̀⌄•́๑)૭
٩(ˊᗜˋ*)و
(ノ°ο°)ノ
(´இ皿இ｀)
⌇●﹏●⌇
(ฅ´ω`ฅ)
(╯°A°)╯︵○○○
φ(￣∇￣o)
ヾ(´･ ･｀｡)ノ"
( ง ᵒ̌皿ᵒ̌)ง⁼³₌₃
(ó﹏ò｡)
Σ(っ °Д °;)っ
( ,,´･ω･)ﾉ"(´っω･｀｡)
╮(╯▽╰)╭
o(*////▽////*)q
＞﹏＜
( ๑´•ω•) "(ㆆᴗㆆ)
😂
😀
😅
😊
🙂
🙃
😌
😍
😘
😜
😝
😏
😒
🙄
😳
😡
😔
😫
😱
😭
💩
👻
🙌
🖕
👍
👫
👬
👭
🌚
🌝
🙈
💊
😶
🙏
🍦
🍉
😣
Source: github.com/k4yt3x/flowerhd
	

	

		
颜文字
Emoji
小恐龙
花!
	


									

			

			
			
		

	






上一篇
下一篇