[toc]
这大概是最后一份用Markdown写的算法笔记,之后的笔记都用iPad写电子笔记了
P5431 【模板】乘法逆元 2(离线线性求逆元科技)
假设我们需要求 $a_1, a_2, \ldots ,a_n$ 的逆元,令 $A = a_1a_2\ldots a_n$,则$a_1^{-1} a_2^{-1} \ldots a_n^{-1} = (a_1a_2\ldots a_n)^{-1} = A^{-1}$,于是我们只需要一次快速幂或者 ExGCD 求出 $A$ 的逆元,维护出 $a$ 的前缀积 Pre 和后缀积 Suf,则 $a_i^{-1} = Pre_{i-1} \cdot A \cdot Suf_{i+1}$,时间复杂度$\mathcal O(n + \log P)$,空间复杂度 $\mathcal O(4n)$
容斥原理
形式化的用法

CF547C Mike and Foam
容斥原理基本应用,容斥每个质因子,Cnt[i]表示含有因子i的数的个数
莫比乌斯反演

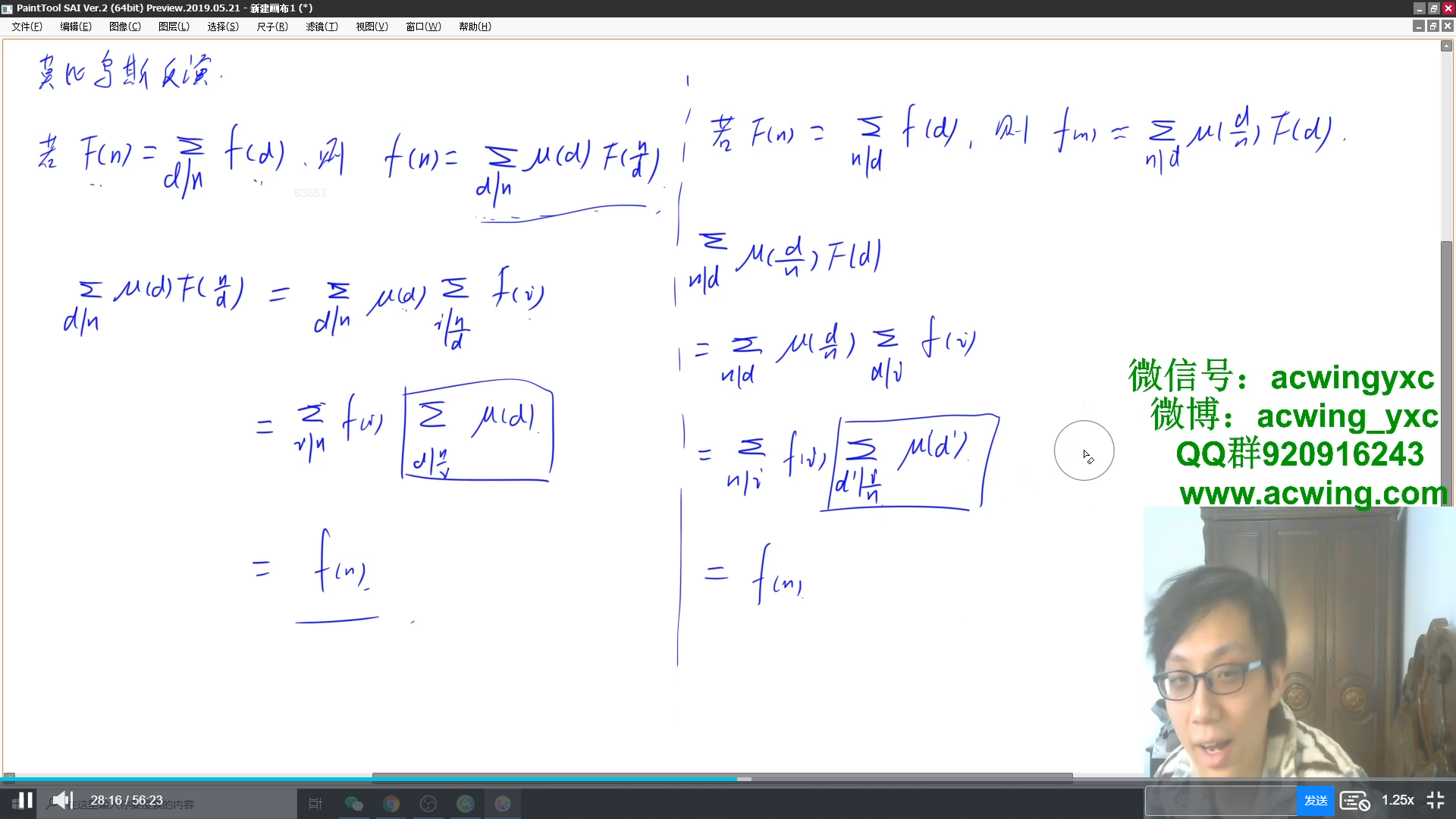
莫比乌斯反演定理的证明,讲的挺好的
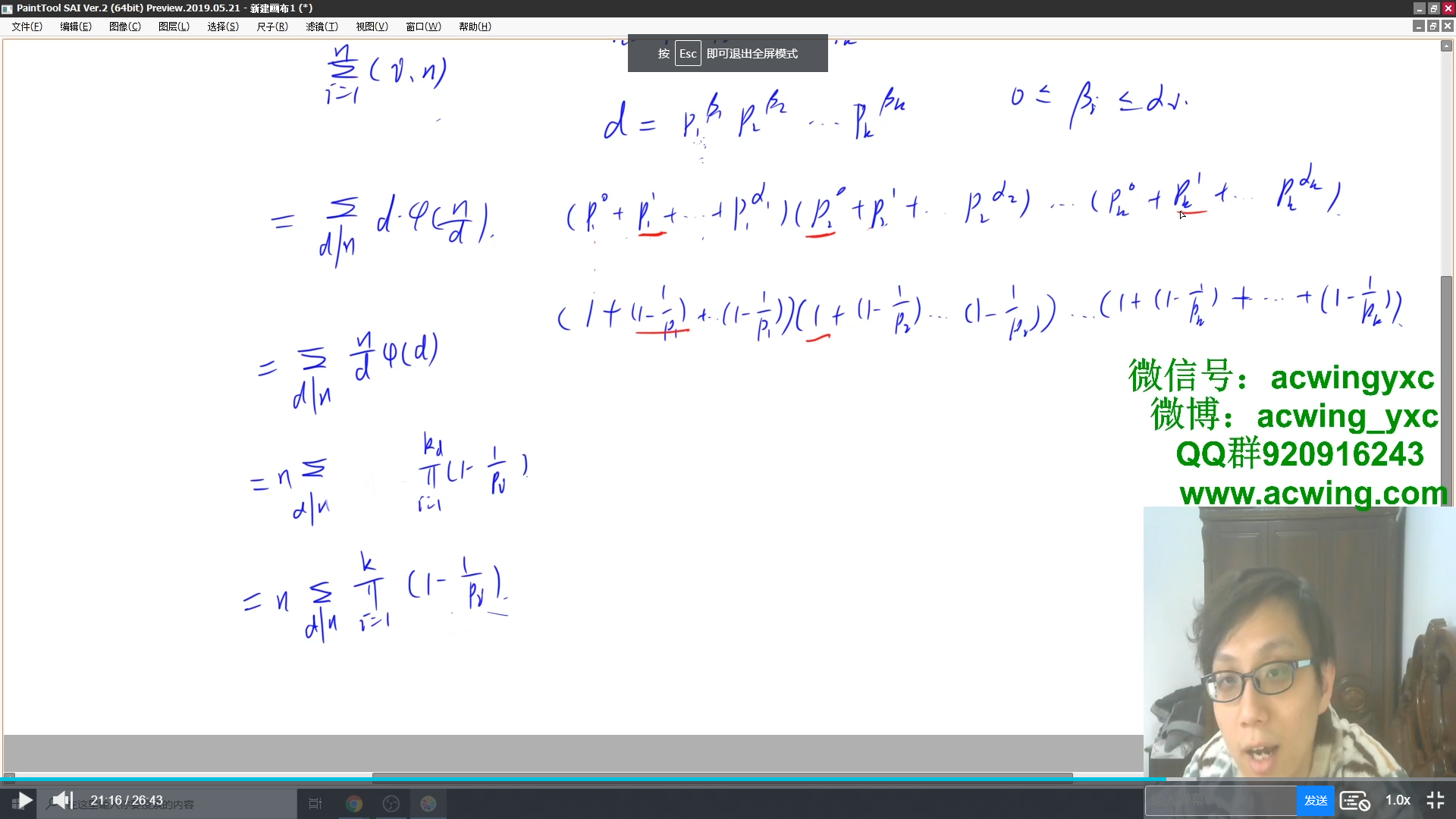
约数个数和


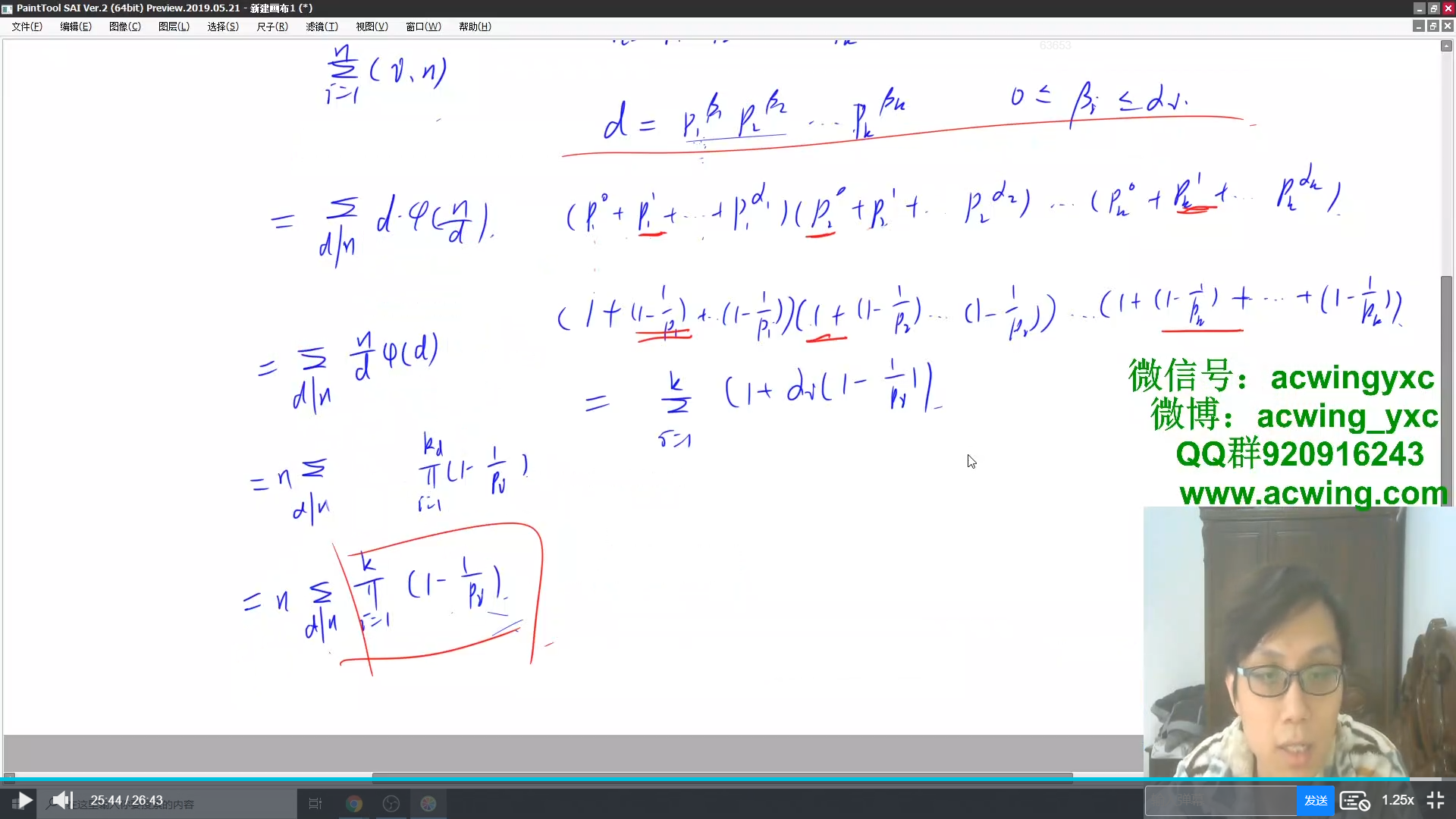
积性函数
龙哥的问题
生成函数
食物
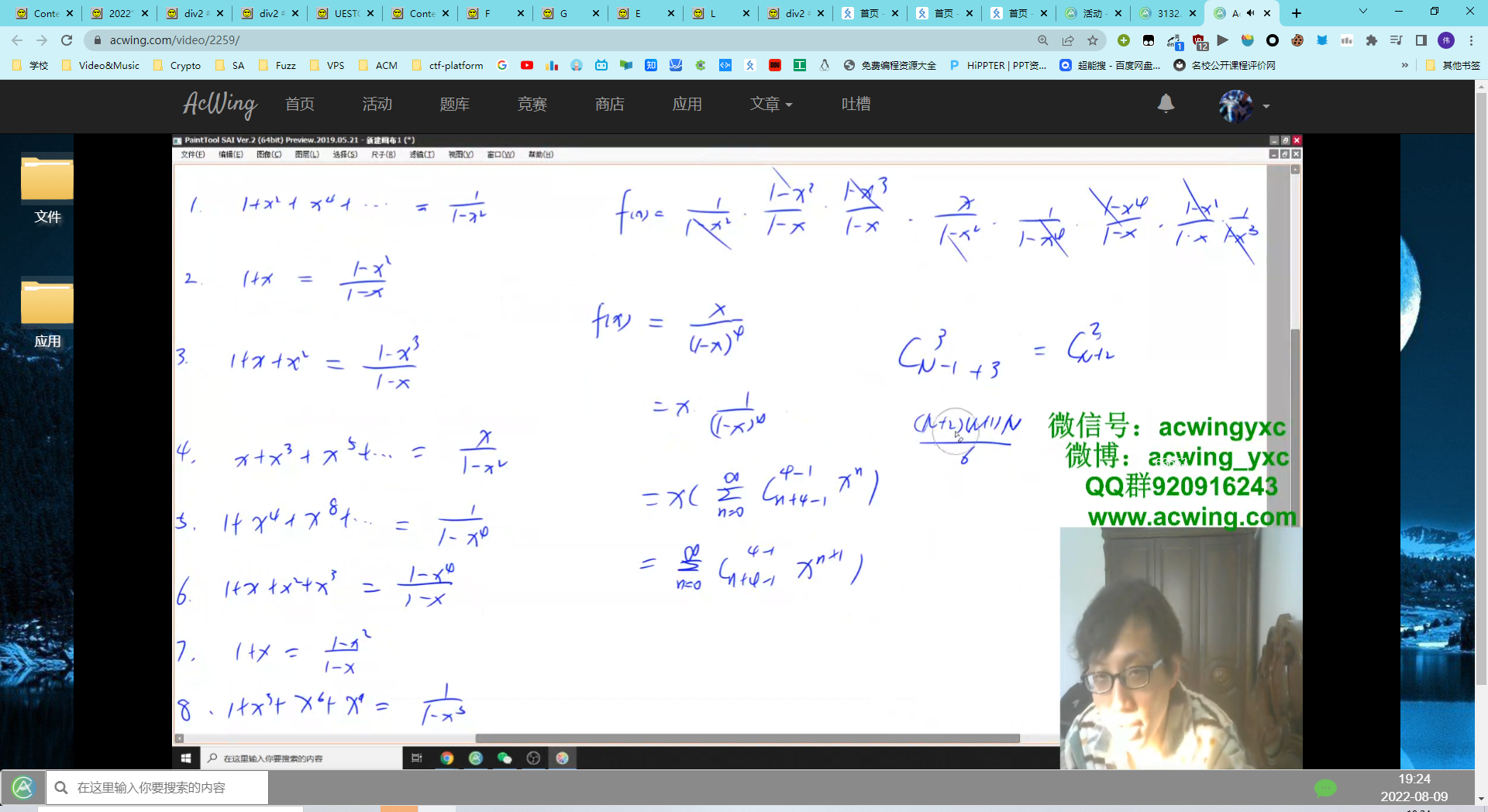
多项式全家桶
NTT的一个坑点
计算$\ A(x) \cdot B(x) \bmod x^n$,其中$\ A(x), B(x)$ 都是$\ n\ $项(即$\ \bmod x^n\ $意义下)多项式,不能只取$\ n\ $个点值,因为我们在进行点值相乘的时候,我们是用$\ A(x), B(x) \bmod x^n\ $的精确点值相乘,得到的是$\ A(x) \cdot B(x) \bmod x^{2n}\ $的精确点值,而不是$\ A(x) \cdot B(x) \bmod x^{n}\ $的精确点值,所以做逆变换得到的多项式就是错误的
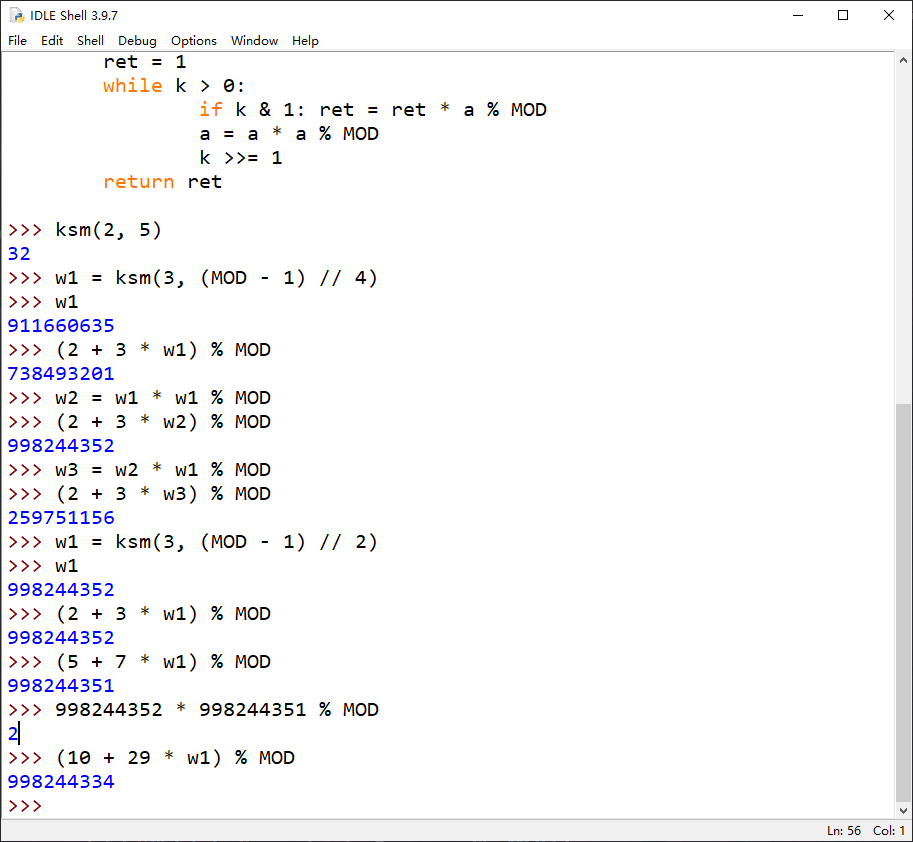
例如上面的例子:
$$
(2+3x)\cdot(5+7x) \equiv 10 + 29x \pmod {x^n} \
(2+3x)\cdot(5+7x) \equiv 10 + 29x + 21x^2\pmod {x^{2n}}
$$
而上面a[0] * b[0] = 5 * 12 = 60,恰是多项式$\ 10 + 29x + 21x^2\ $在1处的点值,而我们希望的点值是29 + 10 = 39,从下图可以看到,如果我手动改下程序算出来的新多项式的点值,就能逆变换得到正确结果:
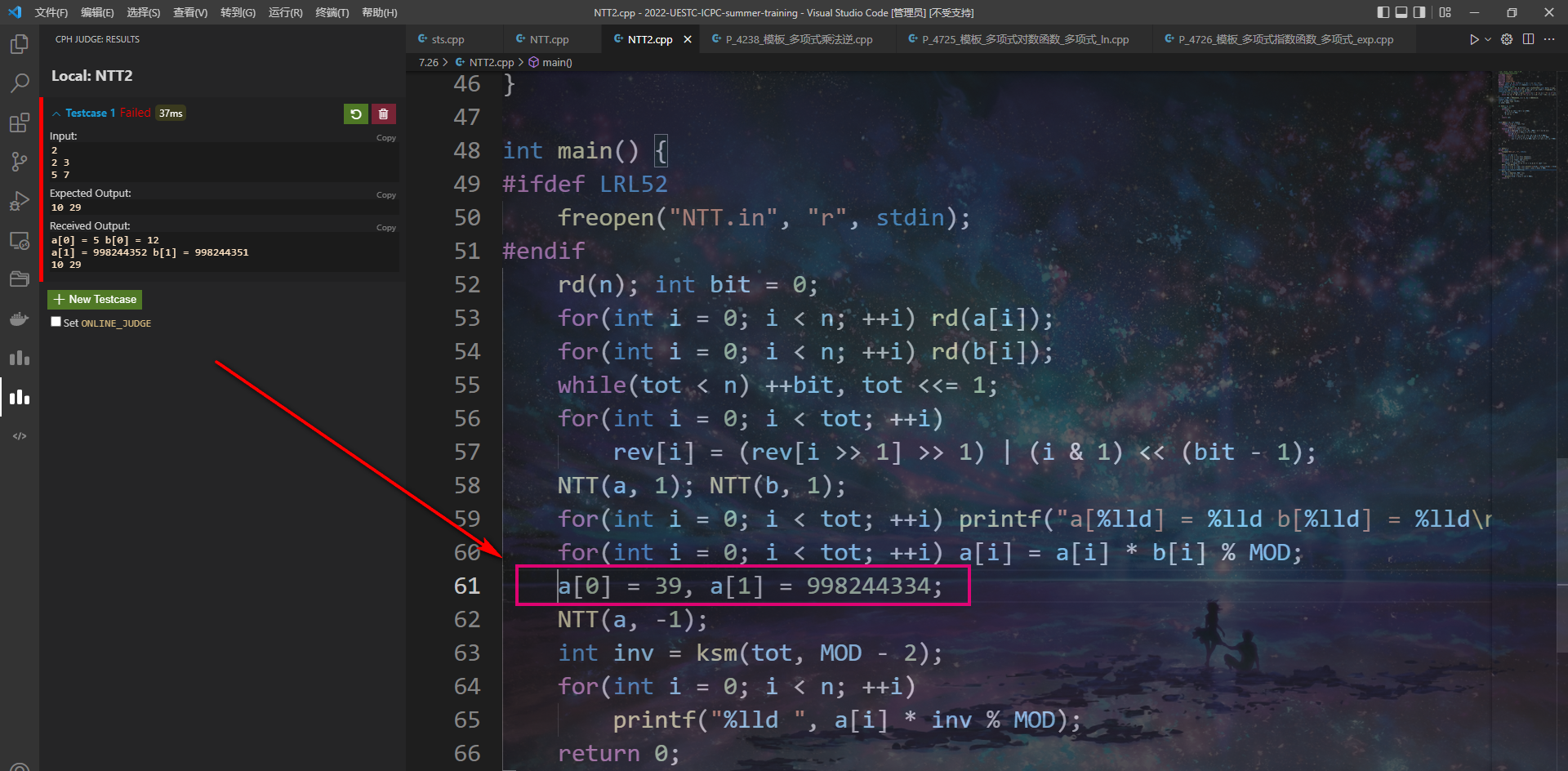
1 998244347 0 0
1 998244347 33 0 0 0 0 0
1 998244347 33 998244169 1020 0 0 0 0 0 0 0 0 0 0 0
1 998244347 33 998244169 1020
注意:NTT一定要保证实际计算的两个多项式乘积的最高次项系数 < tot
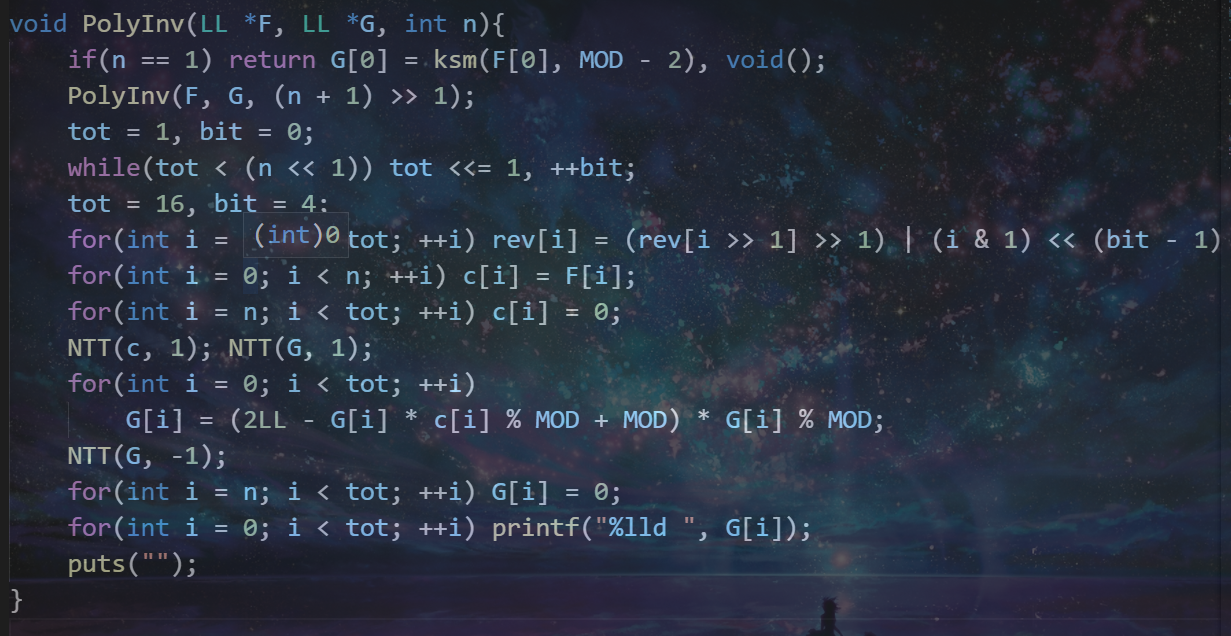

回到那个困惑我大半天的问题为啥要保证G数组是清空的啊,为啥每次做完了G数组要清空,
实际上牛顿迭代法和普通的推导求逆求出的$\ H(x)\equiv F^{-1}(x) \bmod {x^{\frac{n}{2}}}$确实不需要要求$\ H(x)\ $系数大于等于$\ \frac{n}{2}\ $的项为0,例如$\ 1+6x\ $在$\ \bmod x^2\ $下的逆是$\ 1-6x\ $,我们求出了$\ 1+6x\ $在$\ \bmod x\ $逆是1,则$\ H(x) = 1\ $,按照$\ G(x) \equiv H(x)\cdot(2 – H(x)\cdot F(x)) \pmod {x^n}\ $进行计算,可以得到$\ G(x) = 1\cdot (2 – 1\cdot (1 + 6x)) = 1 – 6x\ $,固然正确,但如果$\ H(x) = 1 + 5x\ $,这样计算的结果是$\ G(x) = (1+5x)\cdot (2 – (1+5x)\cdot (1 + 6x)) \equiv 1 – 6x \pmod {x^2}\ $,也是正确的,但在数学上正确却在NTT上不正确,因为实际计算的两个多项式乘积结果的最高次系数>=tot,我们计算出的点值结果也是次数>=tot的多项式的结果,无法逆变换回去了
NTT模数表
NTT模数表(from Fuyuki(uid=109236))
//(g 是mod(r*2^k+1)的原根)
素数 r k g
3 1 1 2
5 1 2 2
17 1 4 3
97 3 5 5
193 3 6 5
257 1 8 3
7681 15 9 17
12289 3 12 11
40961 5 13 3
65537 1 16 3
786433 3 18 10
5767169 11 19 3
7340033 7 20 3
23068673 11 21 3
104857601 25 22 3
167772161 5 25 3
469762049 7 26 3
1004535809 479 21 3
2013265921 15 27 31
2281701377 17 27 3
3221225473 3 30 5
75161927681 35 31 3
77309411329 9 33 7
206158430209 3 36 22
2061584302081 15 37 7
2748779069441 5 39 3
6597069766657 3 41 5
39582418599937 9 42 5
79164837199873 9 43 5
263882790666241 15 44 7
1231453023109121 35 45 3
1337006139375617 19 46 3
3799912185593857 27 47 5
4222124650659841 15 48 19
7881299347898369 7 50 6
31525197391593473 7 52 3
180143985094819841 5 55 6
1945555039024054273 27 56 5
4179340454199820289 29 57 3
分治NTT
利用CDQ分治的思想,对于当前区间[l, r],每次先递归计算左半区间[l, mid],再计算[l, mid]对右半区间[mid + 1, r]的贡献,最后递归计算右半区间[mid + 1, r]
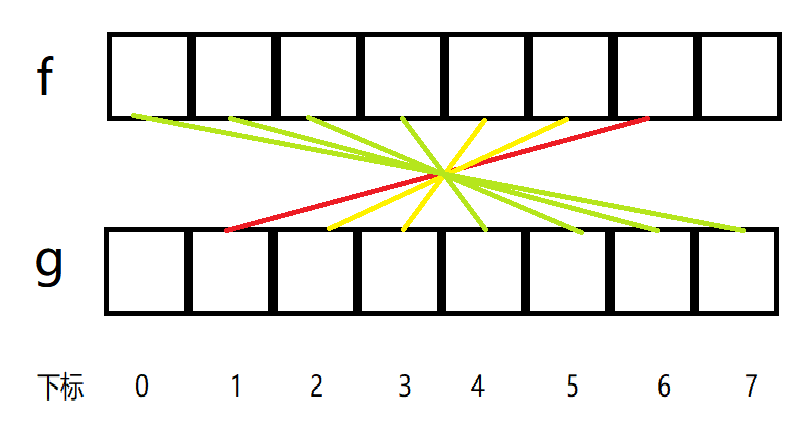
这样只会递归$\log n$层,NTT的总长度为$n\log n$,时间复杂度为$\mathcal O(n\log^2 n)$,思想好理解,但具体细节这里梳理一下:
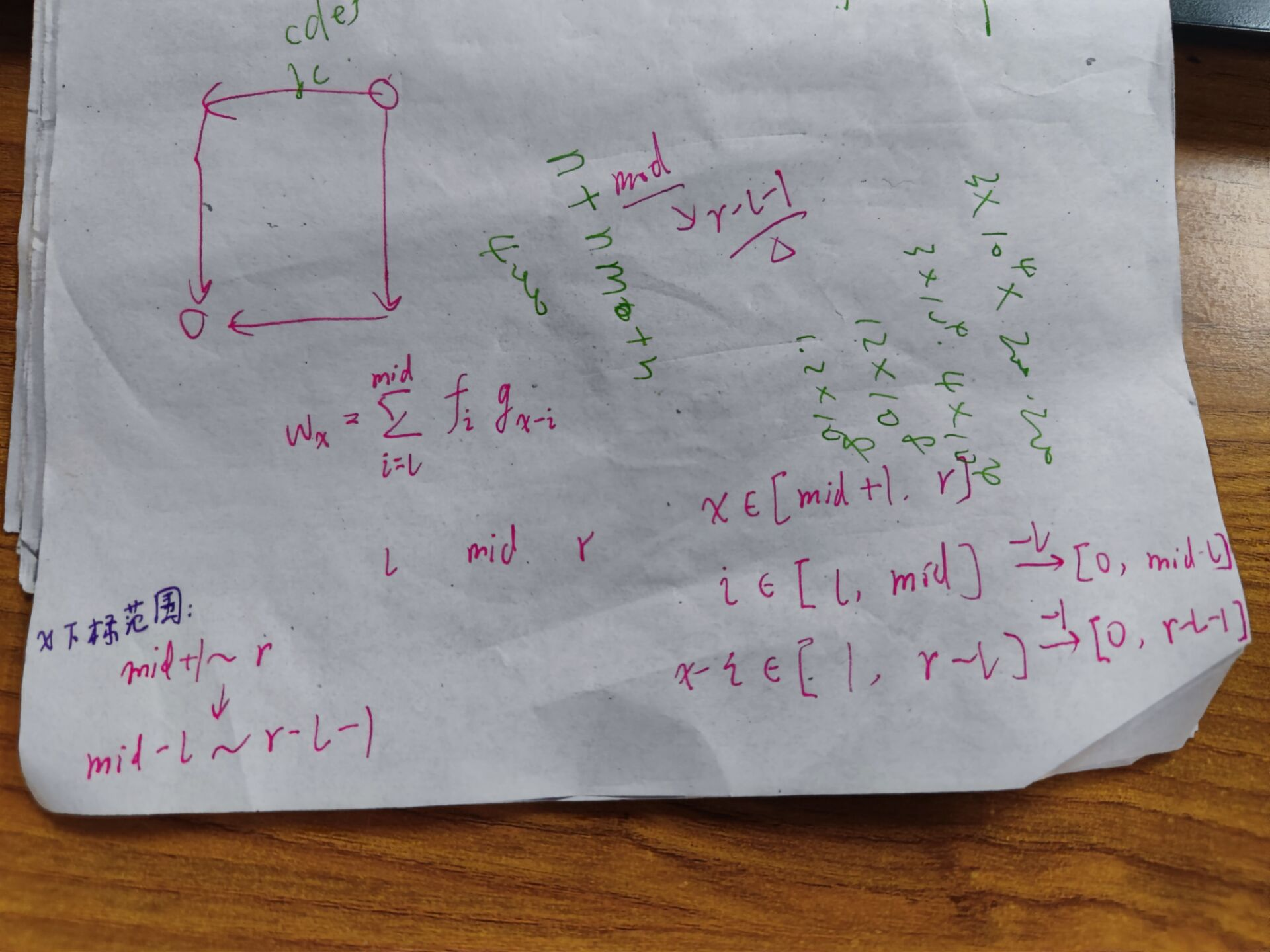
根据上述,左半区间对右半区间位置在$x$的元素贡献为:
$$
\Large w_x = \sum_{i=l}^r f_i g_{x-i}
$$
梳理一下各个变量的范围:
$$
\Large x \in [mid + 1, r], i \in [l, mid] \Rightarrow x – i \in [1, r – l]
$$
P4245 【模板】任意模数多项式乘法
关于使用 CRT 合并后为何在模 $\text{lcm}$ 下有唯一解,参加rxz的exCRT的题解

本题取 3 个质数 998244353, 1004535809, 469762049,计算出结果后再使用 CRT 合并,

Burnside 引理和 Polya 定理
串珠子
魔法手链
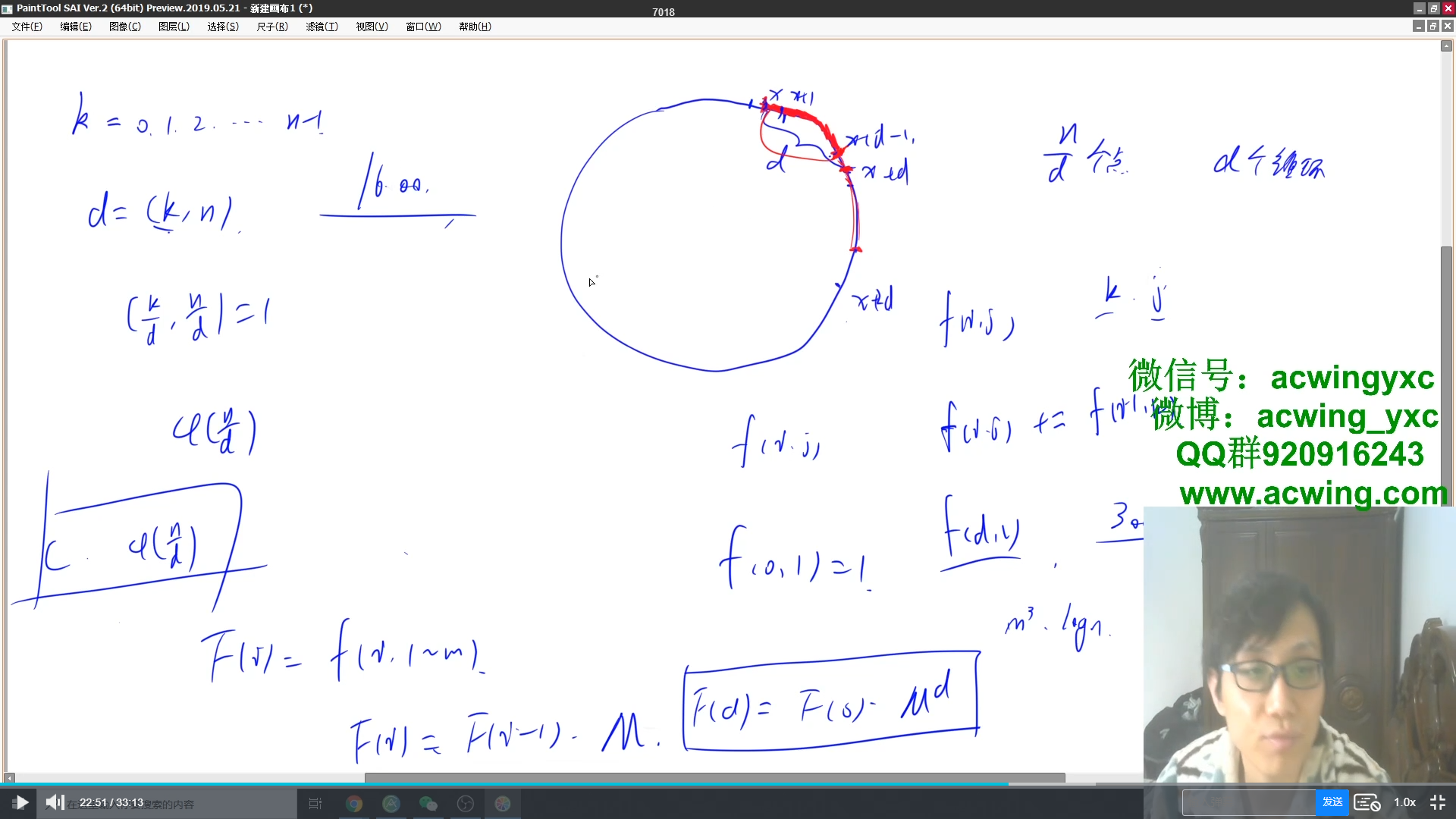
第一类斯特林数
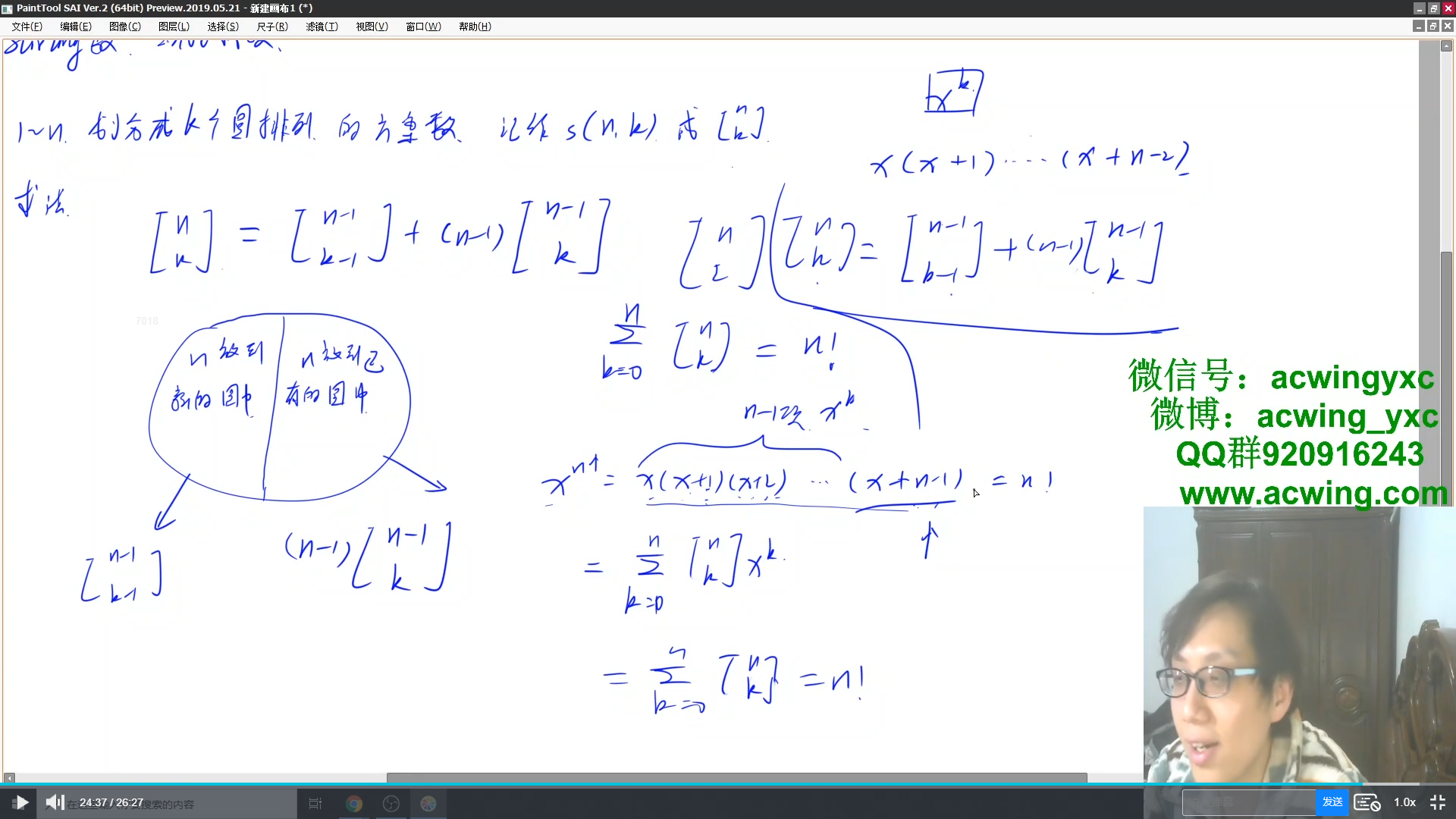
Prufer 序列
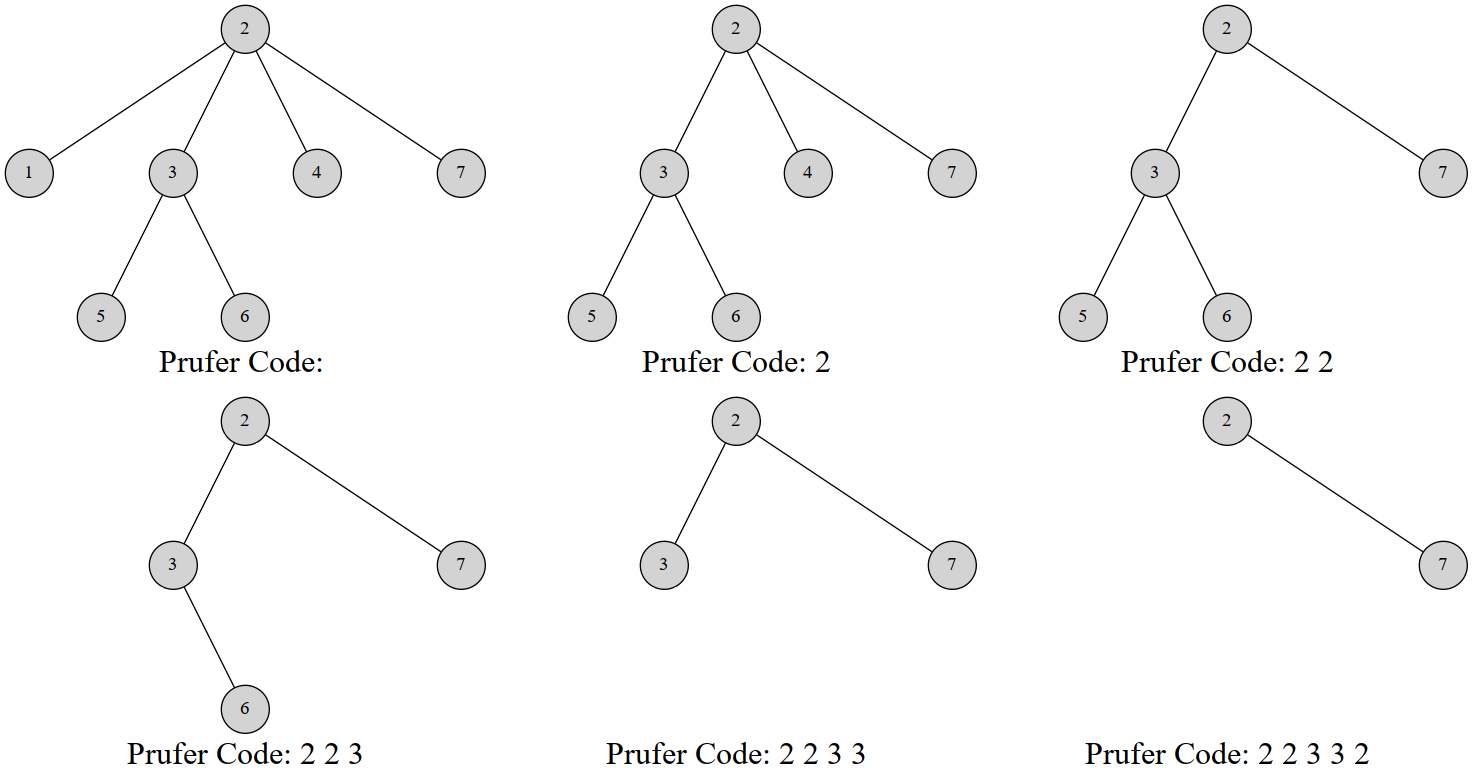
光之大陆
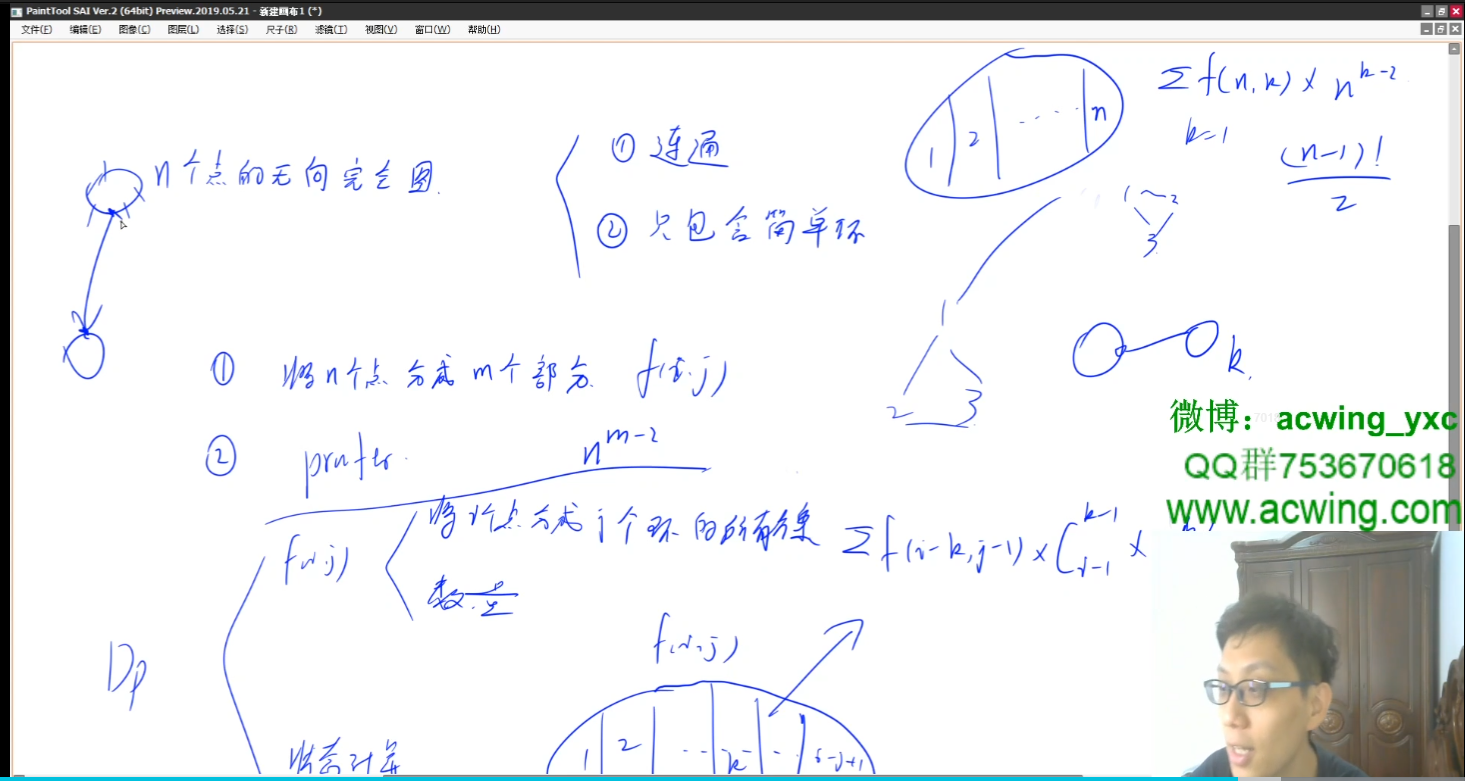
没太懂,那个重复计算是怎么避免的
CDQ 分治
三维偏序
一维排序,二维归并排序,三维树状数组
老C的任务
三维偏序的基本应用,首先将答案写成二维前缀和相减的形式,把询问看作第三维,离线,就变成了三维数点问题
动态逆序对
CDQ分治,下标排序,元素的值归并,时间戳用树状数组。维护时间戳从n ~ 1编号,时间戳越大表示越早被删除
网络流
最小点权覆盖
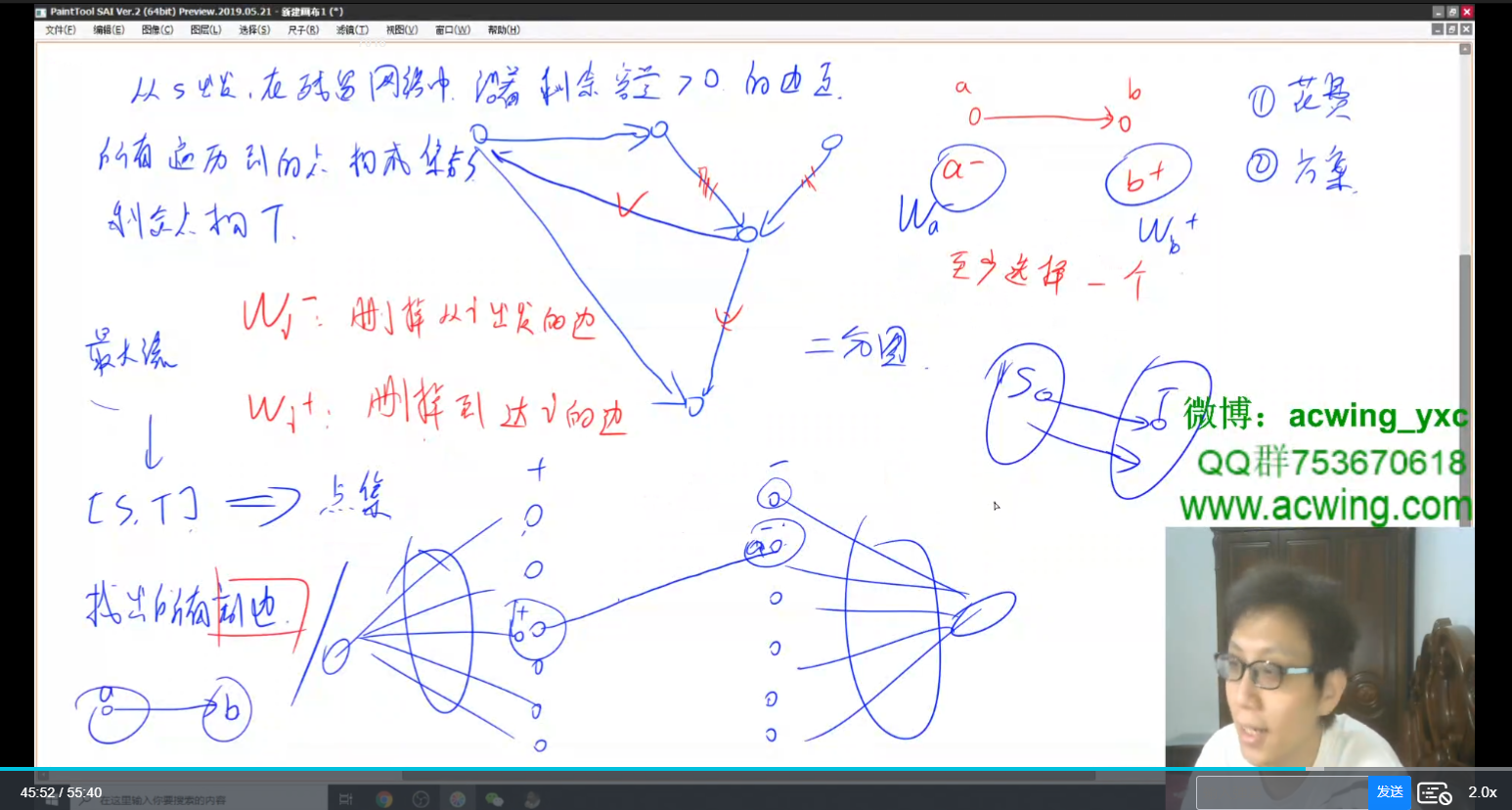
最大密度子图
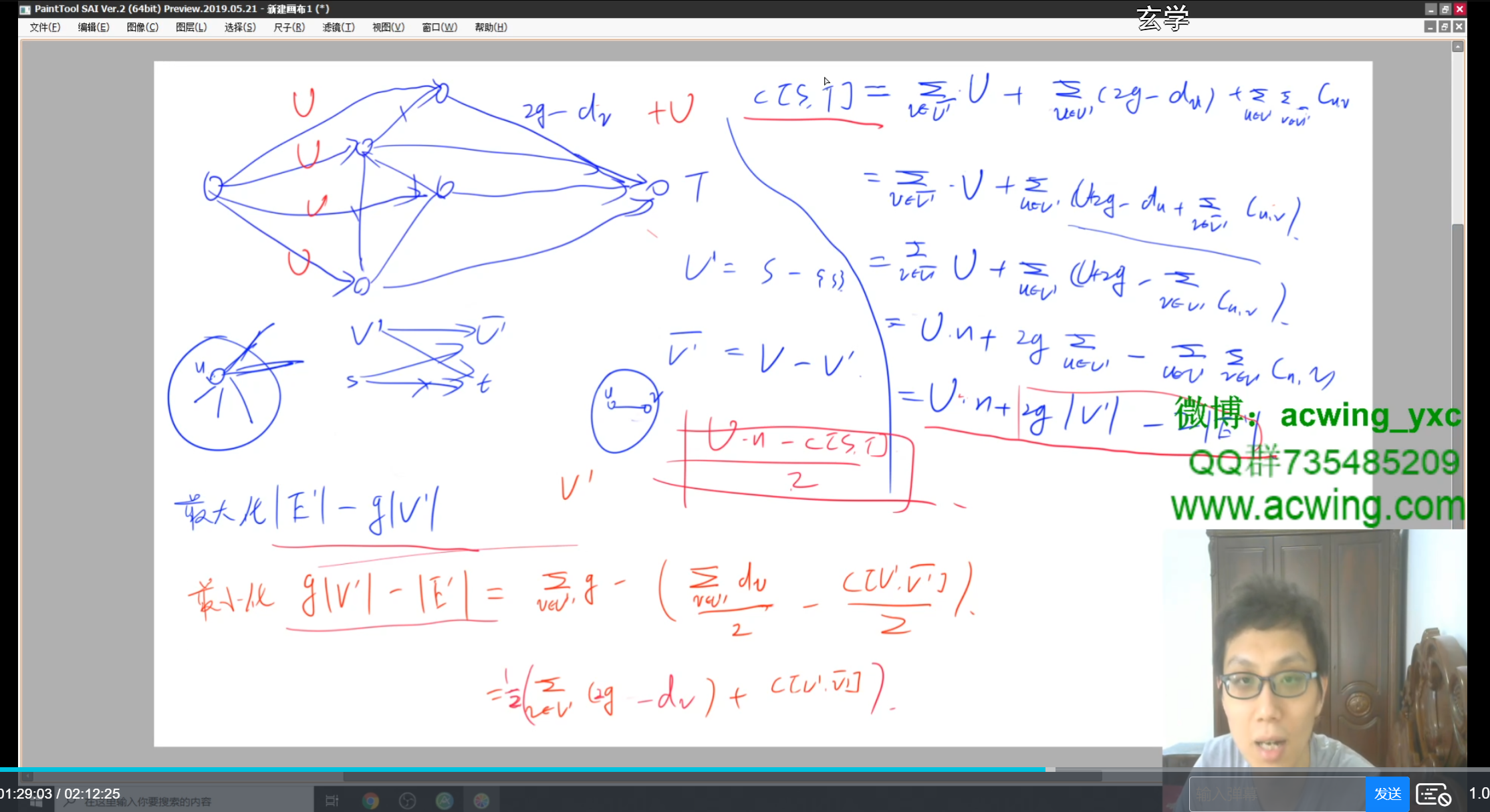
不太理解
牛客概率与期望
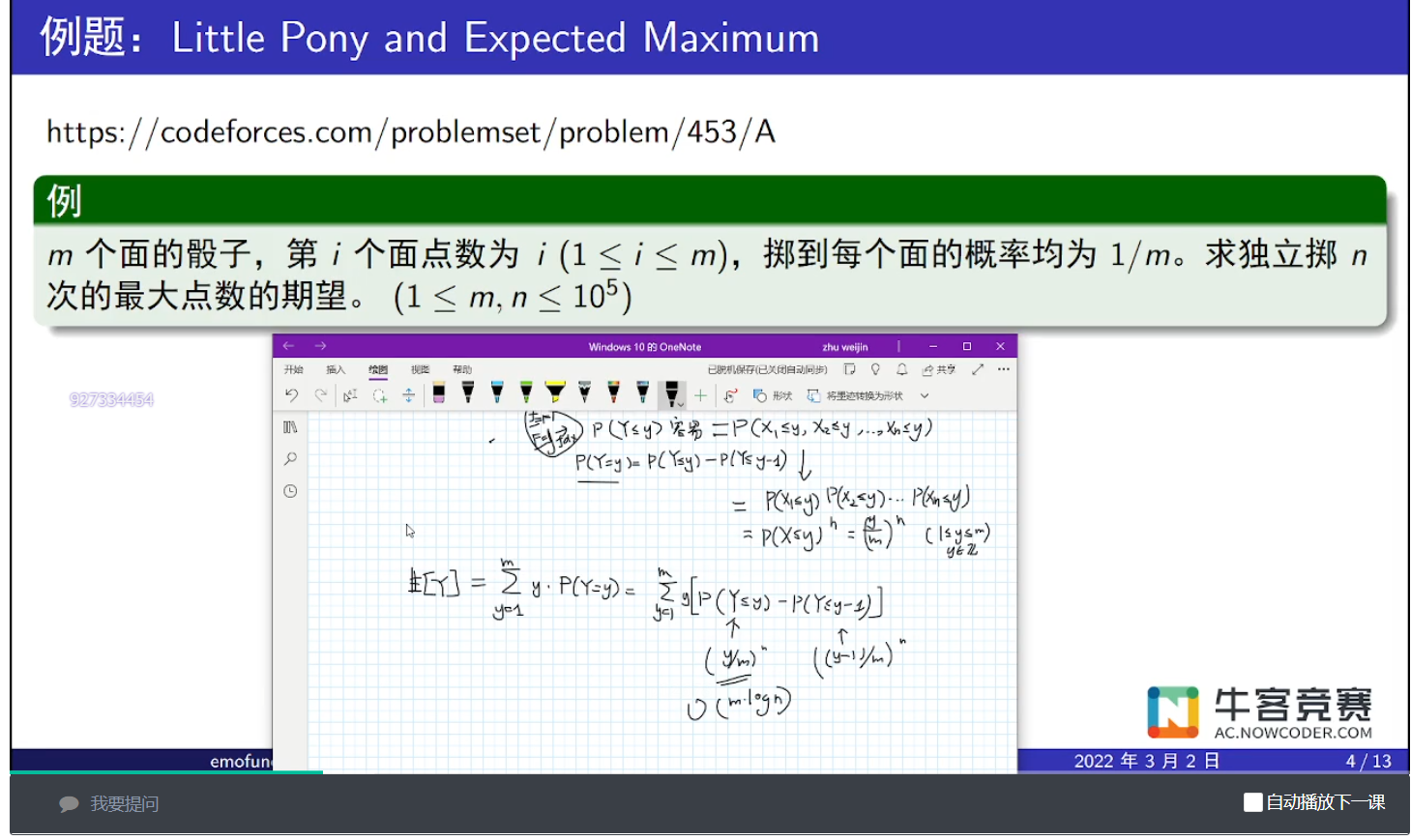
由于群里没有PPT,就只有截图在这里了
擅长解密的小红
如果一次试验成功的概率是 $p$,那么不断重复直到第一次成功需要的期望次数是 $\dfrac{1}{p}$
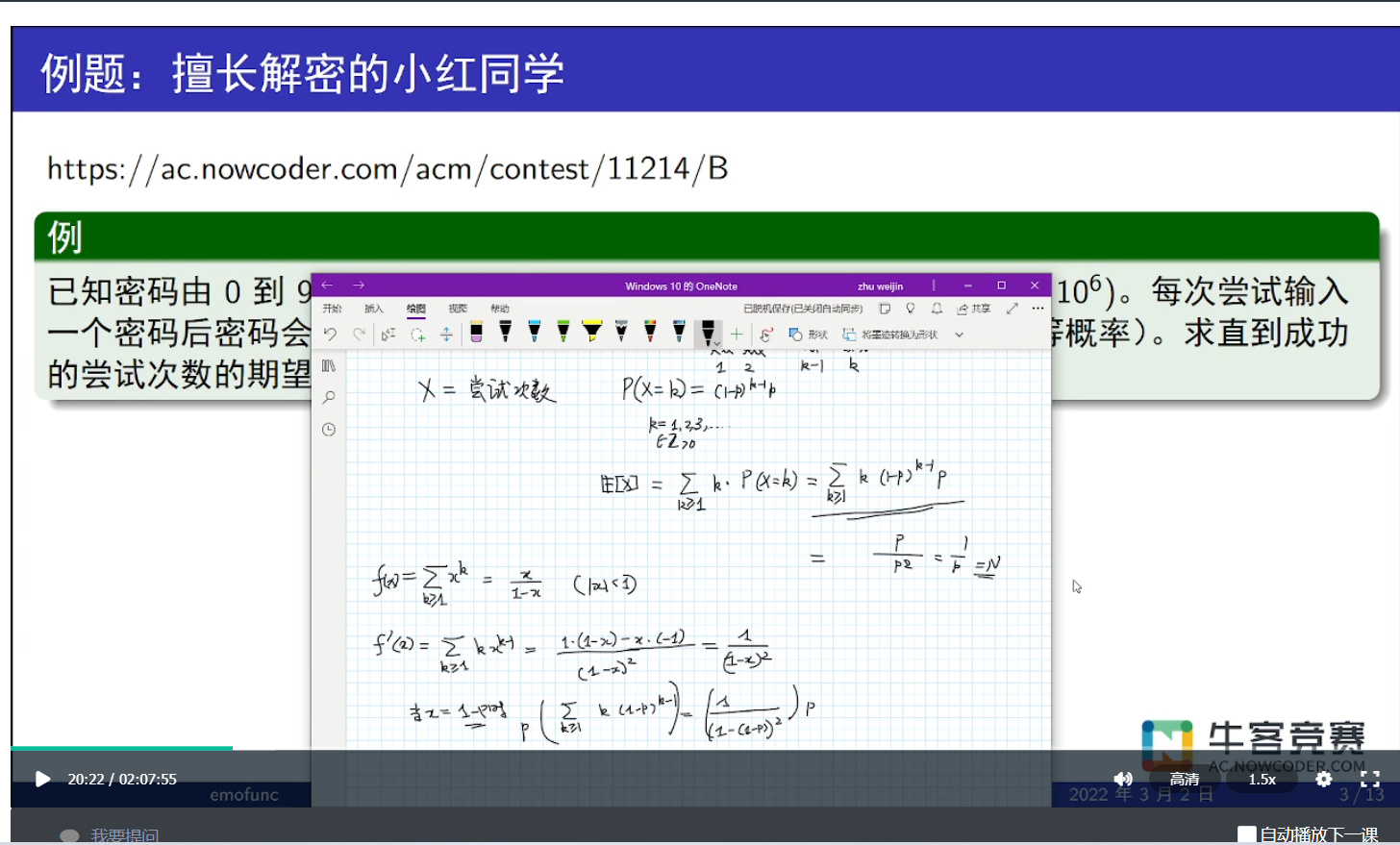
Little Pony and Expected Maximum