[toc]
题解同步发表在Blog上,
有更好的阅读体验~~~
A-蜘蛛的网
一开始没看出来这是啥算法,寻思着最小割也得是有向图吧(后来看到题解没想到可以暴力枚汇点)。
后来感觉可以参考LCA的某道练习题,树上差分,具体地说:
- 求出图中的任意一棵生成树
- 设$cnt_i$表示第$i$边的覆盖次数,枚举所有非树边$(u, v)$,将生成树上$u$到$v$路径上的所有边的覆盖次数$+1$
- $Ans = \min \lbrace cnt_i \rbrace + 1$
以上算法通过50%的数据后WA,思索良久后发现该算法只能计算出割掉1条树边和若干条非树边的最小值,
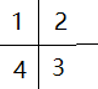
如果最优解的有>=2条树边在生成树上,则无法计算出最优解。例如下图:

蓝色的是生成树的边,我们可以割掉3-5,2-4两条边即可,而这两条边都是树边
不过这个算法虽然是错的,但该有大概率正确,并且复杂度相对很低,当一个算法满足上述条件的时候那我们就考虑 $\text{random_shuffle}$,于是将输入的边的顺序随机化,在时限内尽可能多跑几次就AC了
B-土豆的图
容易发现$d(s, t)$就是最小瓶颈路,即$\text{MST}$上最上$s \rightarrow t$的最大边的权值。然后就比较套路了,在Kruskal求解的过程中,每次合并两个连通块的时候,对于新加入的边$w_i$,所有跨越新加入的边的两点(来自不同连通块的两点)的$d(s, t) = w_i$。开n个vector当平衡树用,每次暴力启发式合并即可。注意L = 0可能会造成计算重复
C-魔法少女
我竟然把这道01BFS的题做成了网络流。
把每个点拆分成入点和出点,入点向出点连流量为1的边,然后如下连边:
if (s[j] == '\\') {
Adde(out_node(i, j), in_node(i + 1, j + 1), 1, 0);
Adde(out_node(i + 1, j + 1), in_node(i, j), 1, 0);
Adde(out_node(i + 1, j), in_node(i, j + 1), 1, 1);
Adde(out_node(i, j + 1), in_node(i + 1, j), 1, 1);
}
else {
Adde(out_node(i, j), in_node(i + 1, j + 1), 1, 1);
Adde(out_node(i + 1, j + 1), in_node(i, j), 1, 1);
Adde(out_node(i + 1, j), in_node(i, j + 1), 1, 0);
Adde(out_node(i, j + 1), in_node(i + 1, j), 1, 0);
}
$\text{out_node(i, j), in_node(i, j)}$分别表示$(i, j)$位置的出点和入点编号
跑一遍费用流即可
D-顶点游走
设$f_{i, j}$表示恰好走过$i$条边后能否到到达$j$号点,
$$
f_{i, j} = \bigvee f_{i-1, k} \and edge(k, j, i -1)
$$
$edge(k, j, i – 1)$表示走过$i – 1$条边后,$k, i$之间有连边,注意到$d_i$的值可能很大,可以将所有点的转移合并写成矩阵布尔积的形式,根据离散数学知识我们知道布尔积也满足结合律,于是矩阵快速幂可以加速计算,使用std::bitset<int>可以减小常数通过本题。
一开始我不知道如何计算出最早到达n号点的时间,感谢钟著晖$n$连自环,再二分的$idea$,后来我实现的时候发现答案只可能在产生新的可走道路后再走$n$次以内,就不用二分了,少一个log,最后$\mathcal O(\dfrac{n^3 c\log d }{W})$解决本题,$W$为std::bitset<int>$带来的常数优化。
就是数据给的很绕,d还不是严格递增的
E-修道路
可以发现点双的有一个性质,从点双上一个点进去,再从点双上另一个点出来,经过的简单路径上可以包括点双上的任意一个你想经过的点(注意:不是说路径包含点双上所有点,是你想经过哪个点都可以),将原图点双缩点,点双缩点后的值用该点双里面的最小点权代替,缩点后是一棵树,最后$\text{DFS}$求出1号点到每个点的路径上的点权最小值即可。
坑点:1. 终点是1号点的时候输出a[1] 2. 点双缩点N, M开2倍空间!!! 3. Lutece assert报错是MLE不是RE
(当然如果点双缩点的时候建出圆方树,就没有第1个坑点了)
F- 开会了
差分约束模板
对于条件$a_u – a_v \le w$,连边$v\stackrel{w}{\longrightarrow}u$,再建立超级源$S$,$S$向每个点连权值为0的边,最后以$S$为起点跑最短路,如果没有负环,则有解,反之无解
G- 二分图匹配
考虑一组配对$( d_j , c_i)$,如果 $d_j > c_i$ ,那么其对期望的贡献为 $\dfrac{w_i}{n!}$
包含该配对的方法有$ (n-1)!$ 种方式,因此其对期望的贡献为 $\dfrac{w_i}{n}$
我们此时能发现最终答案乘 n 一定是一个正整数。
那么对于一组配对$(a_i, b_j)$,其对期望的贡献为
$$
\sum_{a_i + b_j > c_k} w_k
$$
把上式的值作为$i \rightarrow j + n$连边的权值即可,然后就转化为二分图带权匹配问题了
于是复制个费用流的板子跑喜提TLE,也是无语了
按照《算法进阶指南》的讲解写了一发了KM算法交上去依然TLE,过的数据还更少了
经过$\text{Llf0703}$的提醒,发现书上的板子有点小问题,常数有点大,把更新顶标的过程移到dfs后,就可以AC了,事实也证明书上写得没错,$\text{DFS}$版的KM算法是$\mathcal O(n^3)$的,并非是PPT上说的$\mathcal O(n^4)$
H- 守护最好的 0
结论:n为偶数时不删去任何边,n为奇数时可以仅删除一点相连的所有边,此时包含最优解
具体证明可以脑补模拟下或者见题解PPT
奇数个点时建圆方树,$\text{DFS}$计算出每棵子树的size大小和权值和,就可以$\mathcal O(n)$计算出删去每个点的后的答案,总时间复杂度$\mathcal O(n)$
I-又开会了
2-SAT问题
有$N$个变量,每个变量只有两种可能的取值。再给定$M$个条件,每个条件都是对两个变量的取值限制。求是否存在对$N$个变量的合法赋值,使得$M$个条件均满足。这个问题被称为$\text{2-SAT}$问题。$\text{SAT}$是英文$satisfiability$的缩写,意为可满足性。
Solution
设一个变量 $A_i(1 \le i \le n)$ 的两种可能取值分别是 $A_{i,0}$ 和 $A_{i,1}$ 。在 $\text{2-SAT}$ 问题中,$M$ 个条件都可以转化为统一的形式——”若变量 $A_i$ 赋值为 $A_{i, p}$ ,则变量 $A_j$ 必须赋值为 $A_{j,q}$ “,其中 $p, q \in {0, 1}$ 。
$\text{2-SAT}$ 问题判定方法如下:
- 建立$2N$个节点的有向图,每个节点 $A_i$ 对应两个节点,一般设为 $i$ 和 $i + N$ ,分别表示 $A_i = A_{i,0}$ 和 $A_i = A_{i,1}$
- 考虑每个条件,形如”若变量 $A_i$ 赋值为 $A_{i, p}$ ,则变量 $A_j$ 必须赋值为 $A_{j,q}$ “, $p, q \in {0, 1}$ 。从 $i + p \times N$ 到 $j + q \times N$ 连接一条有向边
- 用 $\text{Tarjan}$ 算法求出有向图中的所有强联通分量
- 若 $\exists i \in [1, N]$ 使得 $i $ 和 $i+N$ 属于同一个强联通分量,则表明:若变量 $A_i$ 赋值为 $A_{i,p}$,则变量 $A_i$ 必须赋值为 $A_{i,1-p}$ $(\forall p \in [0, 1])$。 这显然是矛盾的,说明是无解。若不存在这样的 $i$,则问题一定有解。
时间复杂度$\mathcal O(N +M)$
回到本题,$a_u = x$ 和 $a_v = y$ 两者至少有一个成立,即
$$
a_u = x \or a_v = y\
\Rightarrow
\begin{cases}
a_u \ne x \Longrightarrow a_v = y \
a_v \ne y \Longrightarrow a_u = x
\end{cases}
$$
例如题目样例,按照上述方法连边(为了更直观,我把点的编号换成了点的实际含义):
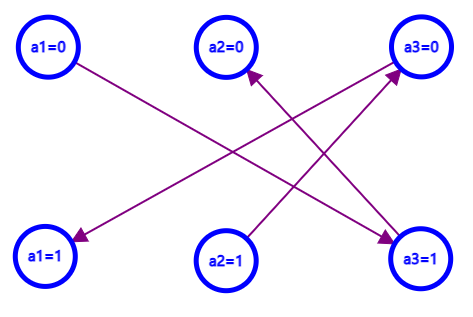
从图中不难看出原题是有解的,且有两组解,分别为$(a_1, a_2, a_3) = (0, 0, 1)$ 和 $(a_1, a_2, a_3) = (1, 1, 0)$ , 实际上对于有解的情况,我们可以通过拓扑顺序构造出一组合法解,即对每个变量 $A_i$ 赋值为结点 $A_{i,0}$ 和 $A_{i,1}$ 中拓扑序靠后的点代表的取值,这样可以避免出现矛盾。
J-tarjan
无向图上的Tarjan全家桶,求割点,桥,点双(注意本题要求点数大于1),然后套板子即可
这部分复习了下《算法竞赛进阶指南》的P396 – P401,讲解和代码都比较清晰透彻,这里就不在赘述了
K- 居民们都住在房屋里
树上两点距离
$$
dis(u, v) = dis(1, u) + dis(1, v) – 2 \times dis(1, \text{LCA(u, v))}
$$
以1为根(可以是其它任意结点),树剖求LCA,DFS一遍求出根到每个点的距离
L-最小生成树
最小生成树计数,经典题
以前是Kruskal合并子树的时候利用乘法原理暴力计算的,这次被卡掉了,遂去学习矩阵树定理


本题即是定理1,
注意到 $\text{MST}$有如下性质:
- 每种权值的边的数量是固定的。
- 不同的生成树中,某一种权值的边任意加入需要的数量后,形成的联通块状态是一样的。
这样一来,我们可以枚举树边的权值 ii,把权值不是 $i$ 的树边都加入图中后进行缩点;对于权值为$i$ 的原图中的边,在缩点后的图中构造基尔霍夫矩阵,用矩阵树定理求出方案数。
最终的答案也是根据乘法原理计算,时间复杂度$\mathcal O(n^3 \log n)$。
M-刺杀卷卷国王
开赛了上来一看K短路,傻乎乎的去抢一血,发现$A*$被卡掉了,遗憾离场(ㄒoㄒ)
后来没时间学习可持久化可并堆了,本题就暂时鸽掉了
N-摆摆国的道路修复
最小直径生成树
第一次学,参照Oi-Wiki-最小直径生成树的讲解

O-纯白色的少年郎,如今只身在何方
单源最短路模板,Dijkstra,没啥好说的
P-哈密顿回路
根据题解,不难理解对于所有图左上角到每个特殊格子的左上角的最短路径上的边,一定是在哈密顿回路里的
在热心群友的帮助下理解了后半部分的题解,这里借一下zzh大佬的样例图建图示意:
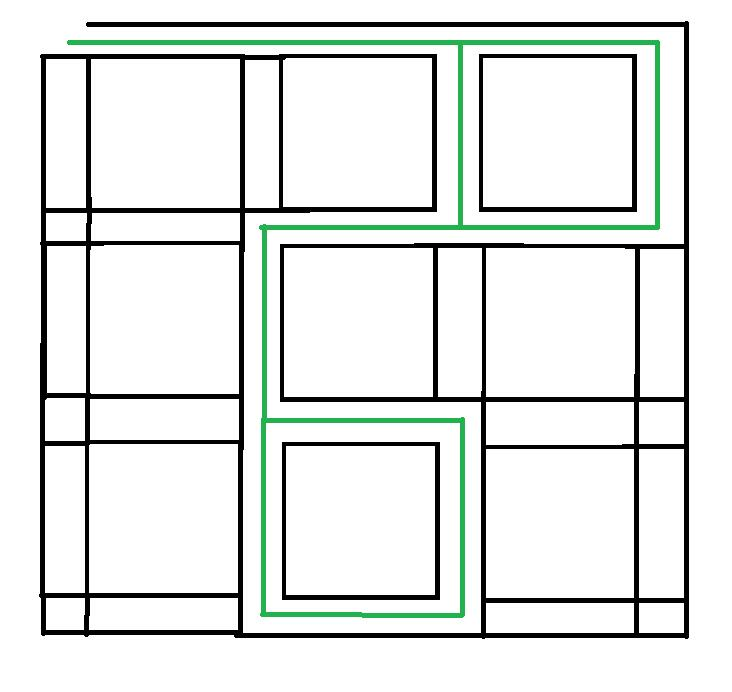
具体实现起来有点麻烦,我代码写得不太优美,有点长,具体说来如下:
- 按原图连边,跑(1,1)到每个特殊格的最短路,并用pre数组记录下最短路上每个点的前一个点
- 拆点建新图,设$(x, y, k)$表示$(x, y)$格点拆分后$k$方向后的点的编号,:
- 将每个特殊格最上角的点到起点的最短路路径的边处理一下,删除最短路径上的跨越边,保证不被割断
- 删除特殊格外圈连向内圈的边
- 删除边$(1, 1, 1) \rightarrow (1, 1, 4)$和$(1, 1, 1) \rightarrow (1, 1, 2)$
- 在新图上以$(1, 1, 2)$为起点跑最短路,答案即是$dis[(1, 1, 4)]$
感觉思路和代码都没问题,但交上去第10个点WA,我检查代码检查了很久也没找出错,求助群友群友表示没坑,苦于没有std也无法对拍,只能等专题结束后求个std对拍一下
Q-建设道路
开始想了一个错误做法:
由于最后所有点都会在生成树中,那么肯定有$\sum_{i=1}^n a_i$的贡献,然后在模仿Prim的贪心,对于已经加入生成树的结点i和未加入生成树的结点j,加入j的代价就是$|j-i| \times D + a_i$(因为$a_j$的贡献已经提前计算了),这样边的式子中就没有了$a_j$,每次只需要找出最小的$i$即可,可以用multiset维护一下。
上面做法错误的原因是它会把无向边变为有向边,$u \rightarrow v$和$v \rightarrow u$d的边的代价是不一样的,这就好像变成了最小树形图了,然而1e5的数据+完全图 ,最小树形图的板子肯定是跑不出来的
最后参照题解,分治优化建图,再跑Kruskal或Prim即可
R-建设道路2
最小树形图,朱刘算法
第一次学,参照洛谷P4716 【模板】最小树形图的题解学习
贴张图,具体算法这里就不赘述了
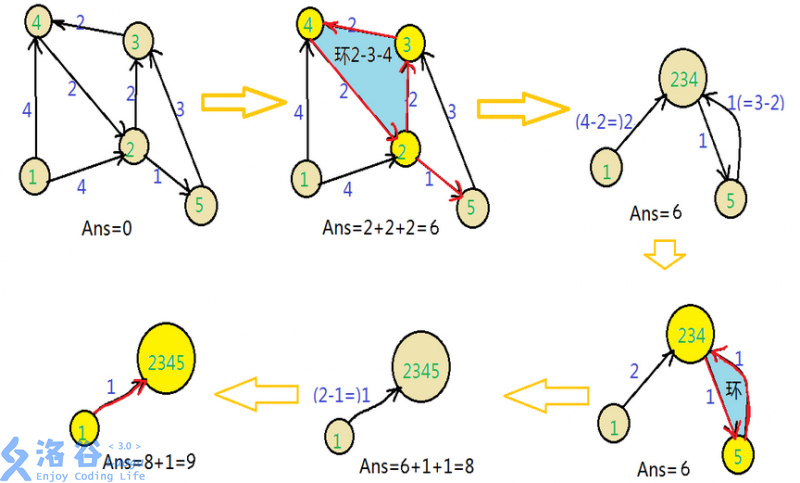
S-合作共赢
一般图最大匹配,带花树
没时间学带花树了,好像这题可以乱搞过
T-我彻底理解了V圈!
网络流,最小路径覆盖
最小路径覆盖=点的总数-网络最大流
拆点后源点向1\~n连接权为1的边,n+1~2n向汇点连权为1的边。
对于原图中相连的两个点$x \rightarrow y$,二分图中体现为$x \rightarrow y + n$。
跑最大流即可