6.1810 Lab8 lock: Parallelism/locking
|
|
351
|
0
|
6.1810,操作系统
|
admin52

3067 字
|
34 分钟
本文最后更新于 218 天前，内容如有失效请评论区留言。

由于各种原因导致这个 Lab 拖了很久（看 fs 那一章花了些时间）才完成，这个 Lab 还是有一些 tricky 的，毕竟涉及到并发 BUG 就不是靠单步 GDB 就能够很轻松找到问题解决的。

注意：File System 相关章节的金句摘录留到下一个 fs lab 里再写。

Lab8

Memory allocator

这个 task 是要为 kalloc 分配器实现一个 PER CPU 的 free page lists，从而减少 kalloc 时 🔒 的争用（lock contention），最后要达到在测试中测试前后 test-and-set 的总增量不超过 10，也就是约等于几乎没有争用。

在 Hint 中有一句是：Let freerange give all free memory to the CPU running freerange. 说实话这一句是提示笔者没太能理解，我理解的是初始化时，每个 CPU 应该平均分配可用内存，即 free page lists 的页面数量应该是基本相等的。

在 Hint 中还有一句是：The function cpuid returns the current core number, but it’s only safe to call it and use its result when interrupts are turned off. You should use push_off() and pop_off() to turn interrupts off and on. 我觉得这个关中断也是没有必要的（后面实测也是如此），xv6 代码中关于 myproc() 的实现是这样的：

// Return the current struct proc *, or zero if none.
struct proc*
myproc(void)
{
  push_off();
  struct cpu *c = mycpu();
  struct proc *p = c->proc;
  pop_off();
  return p;
}

在上面这段代码中，关中断是必要的，否则中间可能会发生时钟中断进而导致 CPU 调度，当前 CPU 上可能就没有正在运行的程序或者没有指向切换到内核态之前的用户程序。

但在我们这个实验中不是必要的，PER CPU 更多是起到负载均衡分流的作用，即使拿到 cpuid 后 context 发生了 CPU 迁移，从别的 CPU 链表上取个空闲页也没有什么问题。

因此我的 kfree 一开始实现是下面这样，kfree 会自动把页归还到恰到的 CPU 上，策略是选择空闲 CPU 链表的空闲页最少的 CPU 来归还，这样尽可能实现负载均衡吧，

struct {
  struct spinlock lock;
  struct run *freelist;
  int nfree; // number of free pages
} kmem[NCPU];

// Free the page of physical memory pointed at by pa,
// which normally should have been returned by a
// call to kalloc().  (The exception is when
// initializing the allocator; see kinit above.)
void
kfree(void *pa)
{
  struct run *r;
  int minv = 0x7fffffff, t = 0, i;

  if(((uint64)pa % PGSIZE) != 0 || (char*)pa < end || (uint64)pa >= PHYSTOP)
    panic("kfree");

  // Fill with junk to catch dangling refs.
  memset(pa, 1, PGSIZE);

  r = (struct run*)pa;

  for (i = 0; i < NCPU; ++i) {
    if (kmem[i].nfree < minv) {
      minv = kmem[i].nfree;
      t = i;
    }
  }


  acquire(&kmem[t].lock);
  r->next = kmem[t].freelist;
  kmem[t].freelist = r;
  ++kmem[t].nfree;
  release(&kmem[t].lock);
}

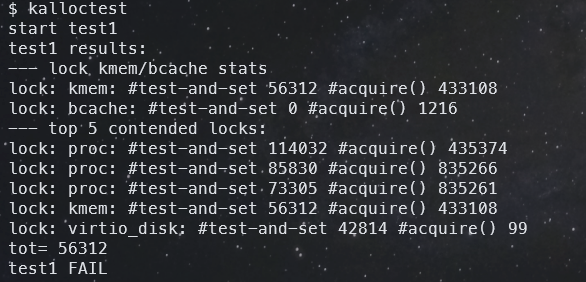
不过这样的测试结果有点出乎我意料，没能通过 test1 ，而且锁争用还很强烈，可以看到 tot=56312，比要求的 10 要高不少了，

image-20241129010442429

通过实践调整代码策略，我意识到 kfree 中 PER CPU 的优化很重要，即每次尽量从当前 CPU 上取，也尽量归还到当前 CPU。只有当页不够时才从其它 CPU 上窃取空闲页。这样我就通过了这个 task。把上面的代码稍微改一下就行了：

// Free the page of physical memory pointed at by pa,
// which normally should have been returned by a
// call to kalloc().  (The exception is when
// initializing the allocator; see kinit above.)
void
kfree(void *pa)
{
  struct run *r;
  int minv = 0x7fffffff, t = 0, i;

  if(((uint64)pa % PGSIZE) != 0 || (char*)pa < end || (uint64)pa >= PHYSTOP)
    panic("kfree");

  // Fill with junk to catch dangling refs.
  memset(pa, 1, PGSIZE);

  r = (struct run*)pa;

  if (!initialized) {
    for (i = 0; i < NCPU; ++i) {
      if (kmem[i].nfree < minv) {
        minv = kmem[i].nfree;
        t = i;
      }
    }
  } else {
    t = cpuid();
  }

  acquire(&kmem[t].lock);
  r->next = kmem[t].freelist;
  kmem[t].freelist = r;
  ++kmem[t].nfree;
  release(&kmem[t].lock);
}

此外，考虑到 NCPU 的值为 8，而 xv6 启动默认为 3 核。因此在当前 CPU 内存不够去其它 CPU 窃取空闲页时，可以从当前 cpuid + 3 的 CPU 上窃取，这样可以减少多个 core 同时内存不够用时的锁争用可能。

这里还用到了一点数论的技巧，由于 $\gcd(3,\ \texttt{NCPU}) = 1$，因此这么做是可行的，总会遍历完所有可用的 CPU。

完整代码

完整实现代码如下：

diff --git a/kernel/kalloc.c b/kernel/kalloc.c
index 0699e7e..d9ec4bf 100644
--- a/kernel/kalloc.c
+++ b/kernel/kalloc.c
@@ -21,13 +21,23 @@ struct run {
 struct {
   struct spinlock lock;
   struct run *freelist;
-} kmem;
+  int nfree; // number of free pages
+} kmem[NCPU];
+
+static char kmem_lock_name[NCPU][10];
+static int initialized = 0;

 void
 kinit()
 {
-  initlock(&kmem.lock, "kmem");
+  int i;
+
+  for (i = 0; i < NCPU; ++i) {
+    snprintf(kmem_lock_name[i], sizeof(kmem_lock_name[i]), "kmem%d", i);
+    initlock(&kmem[i].lock, kmem_lock_name[i]);
+  }
   freerange(end, (void*)PHYSTOP);
+  initialized = 1;
 }

 void
@@ -47,6 +57,7 @@ void
 kfree(void *pa)
 {
   struct run *r;
+  int minv = 0x7fffffff, t = 0, i;

   if(((uint64)pa % PGSIZE) != 0 || (char*)pa < end || (uint64)pa >= PHYSTOP)
     panic("kfree");
@@ -56,10 +67,22 @@ kfree(void *pa)

   r = (struct run*)pa;

-  acquire(&kmem.lock);
-  r->next = kmem.freelist;
-  kmem.freelist = r;
-  release(&kmem.lock);
+  if (!initialized) {
+    for (i = 0; i < NCPU; ++i) {
+      if (kmem[i].nfree < minv) {
+        minv = kmem[i].nfree;
+        t = i;
+      }
+    }
+  } else {
+    t = cpuid();
+  }
+
+  acquire(&kmem[t].lock);
+  r->next = kmem[t].freelist;
+  kmem[t].freelist = r;
+  ++kmem[t].nfree;
+  release(&kmem[t].lock);
 }

 // Allocate one 4096-byte page of physical memory.
@@ -68,13 +91,39 @@ kfree(void *pa)
 void *
 kalloc(void)
 {
-  struct run *r;
+  struct run *r = 0;
+  int cpu, i;

-  acquire(&kmem.lock);
-  r = kmem.freelist;
-  if(r)
-    kmem.freelist = r->next;
-  release(&kmem.lock);
+  cpu = cpuid();
+  if (kmem[cpu].nfree > 0) {
+    acquire(&kmem[cpu].lock);
+    if (kmem[cpu].nfree > 0) {
+      r = kmem[cpu].freelist;
+      kmem[cpu].freelist = r->next;
+      --kmem[cpu].nfree;
+    }
+    release(&kmem[cpu].lock);
+  }
+
+  if (!r) {
+    // This is a trick that uses the congruence property of number theory,
+    // to reduce lock contention when multiple CPUs are trying to allocate
+    // memory simultaneously.
+    // It requires that gcd(3, NCPU) = 1.
+    for (i = (cpu + 3) % NCPU; i != cpu; i = (i + 3) % NCPU) {
+      if (kmem[i].nfree == 0)
+        continue;
+      acquire(&kmem[i].lock);
+      if (kmem[i].nfree > 0) {
+        r = kmem[i].freelist;
+        kmem[i].freelist = r->next;
+        --kmem[i].nfree;
+        release(&kmem[i].lock);
+        break;
+      }
+      release(&kmem[i].lock);
+    }
+  }

   if(r)
     memset((char*)r, 5, PGSIZE); // fill with junk

Buffer cache

这个 task 还是有点 tricky，还是调试和思考了好几个小时最后才完全写正确的。作为笔记，太多心路历程和思考过程就没法在这里一一赘述了。

Hint 里提示我们应该使用哈希表来将整个空闲 buffer cache 分为好几块，每个哈希的 bucket 对应一块，这样可以让锁的更加细粒度，很大程度上减小冲突。由于整个 buffer cache 也就是只有 30 个页，那为了实现简便，我决定用空间换时间，采用一个 buffer cache 页对应一个锁的力大砖飞写法。

但哈希还是没法避免的，由于 30 不是一个质数，直接对 30 取模来实现哈希容易产生哈希冲突，因此我们需要设计个方法将 [1, 2000] 的数（xv6 共有 2000 个 block）随机、均匀地映射到 [0, 30)，哈希函数的设计交给 GPT 老师：

要在 [0, 2000] 范围的整数上构造一个能够随机、均匀地映射到 [0, 30) 的哈希函数，同时避免因因数导致的哈希冲突，我们可以使用乘法哈希法（Multiplicative Hashing）。

使用乘法哈希法，通过一个合适的乘数和位移操作，将输入数均匀地映射到目标范围。这个方法能够有效地打乱输入数的位模式，避免简单取模带来的冲突。

乘法哈希法公式：

$$
h(k) = \left\lfloor m \times (kA \bmod 1) \right\rfloor
$$

  • $k$ 是输入整数。
  • $m$ 是哈希表大小（这里为 30）。
  • $A$ 是介于 0 和 1 之间的常数，通常取黄金比例倒数 ( $A = \frac{\sqrt{5}-1}{2} \approx 0.6180339887$ )。

C 语言实现

#include <stdio.h>
#include <stdint.h>

#define HASH_SIZE 30

unsigned int hash(unsigned int k) {
    // 使用黄金比例倒数作为乘数常数
    const double A = 0.6180339887;
    // 计算 k * A 的小数部分
    double frac_part = (k * A) - (unsigned int)(k * A);
    // 计算哈希值
    return (unsigned int)(HASH_SIZE * frac_part);
}

int main() {
    // 测试哈希函数
    for (unsigned int i = 0; i <= 2000; i += 100) {
        printf("hash(%4u) = %u\n", i, hash(i));
    }
    return 0;
}

解释说明

  1. 使用黄金比例倒数作为乘数常数：
  • 黄金比例倒数 ( $A = \frac{\sqrt{5}-1}{2}$ ) 是一个无理数，能够很好地打乱输入数的位模式，减少冲突。
  1. 计算小数部分：
    • frac_part = (k * A) - (unsigned int)(k * A);
    • 这一步计算了 $kA$ 的小数部分，即 $kA \bmod 1$。
  2. 计算哈希值：

  • hash_value = (unsigned int)(HASH_SIZE * frac_part);
  • 将小数部分放大到 [0, HASH_SIZE) 范围，并取整。
  1. 为什么这样可以避免冲突：
    • 乘法哈希法利用了无理数的性质，使得输入数经过乘法和取小数部分后，均匀地分布在 [0, 1) 区间。
    • 通过乘以哈希表大小 HASH_SIZE，将其映射到 [0, HASH_SIZE)。

改进的整数运算实现

由于在嵌入式系统或不支持浮点运算的环境中，浮点运算可能效率不高，我们可以使用定点数或整数运算来实现。

#include <stdio.h>
#include <stdint.h>

#define HASH_SIZE 30
#define MULTIPLIER 2654435769U  // 这是 Knuth 建议的乘数

unsigned int hash(unsigned int k) {
    return (unsigned int)(((uint64_t)k * MULTIPLIER) >> 28) % HASH_SIZE;
}

int main() {
    // 测试哈希函数
    for (unsigned int i = 0; i <= 2000; i += 100) {
        printf("hash(%4u) = %u\n", i, hash(i));
    }
    return 0;
}

整数实现的解释

  1. 选择合适的乘数：
  • 使用 Knuth 推荐的乘数 2654435769（即 $2^{32} \times \frac{\sqrt{5}-1}{2}$ 的整数部分）。
  • 这个乘数能够很好地将输入数的位模式打乱。
  1. 计算哈希值：
  • (uint64_t)k * MULTIPLIER 将 k 与乘数相乘，结果可能超过 32 位，因此使用 64 位整数。
  • >> 28 右移 28 位，取高位部分，模拟取小数部分的效果。
  • % HASH_SIZE 将结果映射到 [0, HASH_SIZE) 范围。
  1. 为什么右移 28 位：
  • 因为我们使用了 32 位乘数，乘法结果是 64 位。
  • 右移 28 位，相当于取结果的高 36-28=8 位，这部分包含了乘法后高位的变化，能够提供较好的随机性。

有了哈希函数之后，我们可以写代码了。但还需要思考下如何处理哈希冲突？因为 $ 2000 >> 30$ 的，buffer cache 肯定也会不够用的，当同一个哈希值对应多个缓存 buffer 页的时候，我们该如何正确的查找到？经过几次修改后的 bget 实现代码如下。

这里我解释一下里面一段注释，尽管我们一个空闲页对应一个锁，但我们在查询这个 blockno 的缓存页的时候，笔者推迟释放这个锁（尽管下面这个实现是有问题的，但这个设计思想会在后面正确代码中沿用）。考虑这样一种情况，有两个线程都在 bget 同一个 blockno，并且这个 blockno 没有被缓存，那么它们都会尝试寻找一个空闲的 buffer 页来缓存，那么极有可能两个线程会寻找到两个不同的 buffer 页来缓存，这就违背了同一个物理页在缓存页中最多只有一份的规则，就会出现 inconsistency。

// Look through buffer cache for block on device dev.
// If not found, allocate a buffer.
// In either case, return locked buffer.
static struct buf*
bget(uint dev, uint blockno)
{
  struct buf *b;
  int idx, i, j;

  idx = hash(blockno);

  // Is the block already cached?
  for (i = idx, j = 0; j < NBUF; i = (i + 1) % NBUF, ++j) {
    b = &bcache.buf[i];
    acquire(&b->spinlock);
    if (b->dev == dev && b->blockno == blockno) {
      ++b->refcnt;
      release(&b->spinlock);
      if (i != idx)
        release(&bcache.buf[idx].spinlock);
      acquiresleep(&b->lock);
      return b;
    }
    // We defer releasing the idx lock.
    // Consider the case when two threads are searching for the same uncached block,
    // the later one should wait for the former one to finish the allocation. Otherwise,
    // the later one may encounter an empty buffer ealier than the former one. 
    if (i != idx)
      release(&b->spinlock);
  }
  release(&bcache.buf[idx].spinlock);

  // Not cached.
  // Search for an unused buffer.
  for (i = idx, j = 0; j < 10000; i = (i + 1) % NBUF, ++j) {
    b = &bcache.buf[i];
    acquire(&b->spinlock);
    if (b->refcnt == 0) {
      b->dev = dev;
      b->blockno = blockno;
      b->valid = 0;
      b->refcnt = 1;
      release(&b->spinlock);
      acquiresleep(&b->lock);
      return b;
    }
    release(&b->spinlock);
  }

  panic("bget: no buffers");
}

当然这样做有个显而易见的死锁 BUG，在循环的时候同时持有了两个锁，并且获得锁编号的获得顺序又没有作限制，因此死锁在所难免。

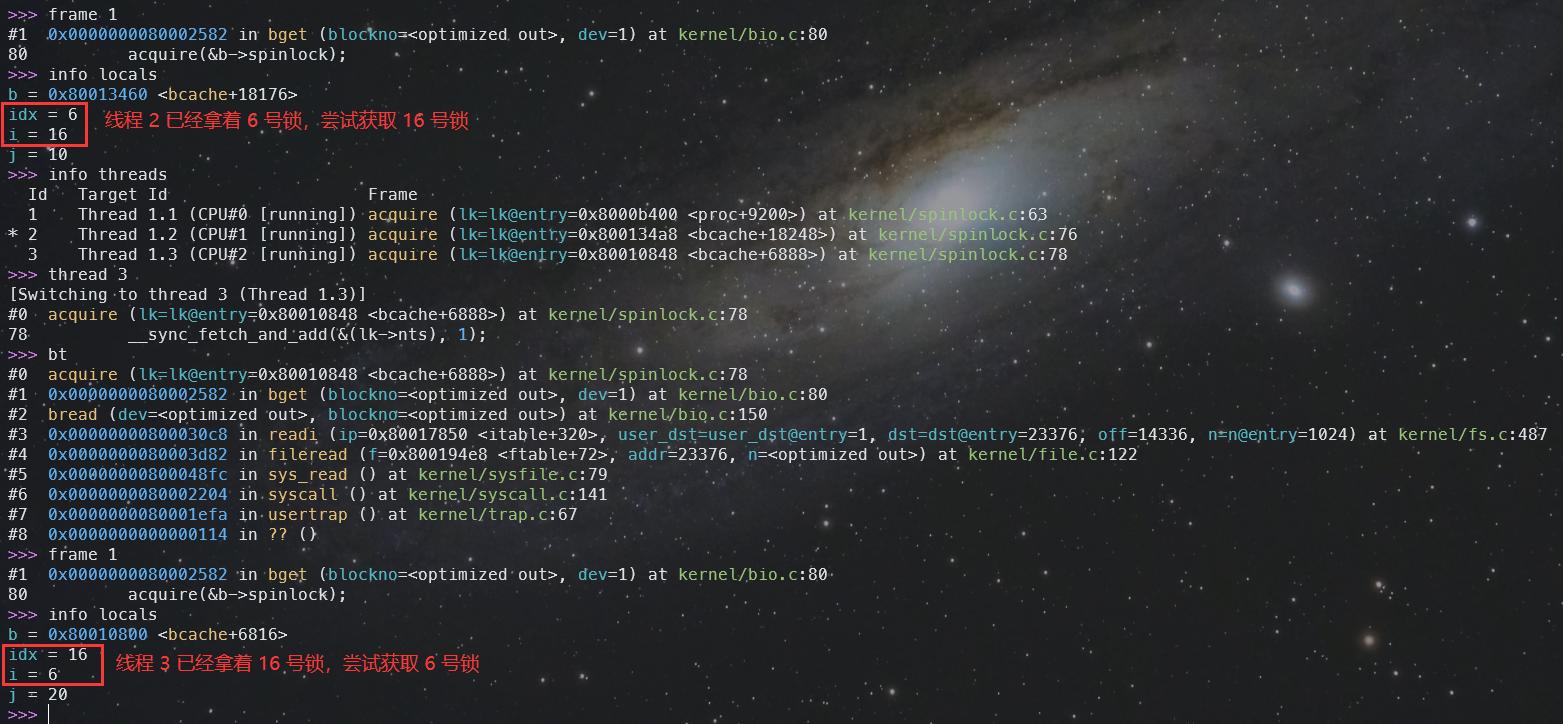
下面讲讲死锁的调试经验。xv6 出现死锁的时候会卡死，这时候在 gdb 中 Ctrl-C 停下，可以看到几个线程都在执行 kernel/spinlock.c 的代码，这时候可以通过 frame 来切换栈帧，查看循环中尝试获取的锁编号，还可以通过 thread 来切换线程。

下图中可以清晰地看到出现死锁的现场，线程 2 已经拿着 6 号锁，尝试获取 16 号锁。线程 3 已经拿着 16 号锁，尝试获取 6 号锁：

image-20241130164451611

解决办法是继续力大砖飞，每个 buffer cache 页用两个锁，一个锁用于保护 struct buf 内的字段修改是原子的，一个锁用于在并发寻找空闲页时阻塞后来的线程。这样的实现笔者认为还是比较高效的，在寻找 cache 页的时候，只会对当前正在遍历的 cache 页上锁，没有其它上锁，因此多个线程可以做到并发寻找已缓存的 cache 页，而不是 Hint 里的 serialize finding 也是 OK 的。并且在哈希值不冲突的情况下，多个线程也可以做到并发寻找空闲 cache 页。

PS: 笔者提早开香槟，第一次测试已经全部通过样例了，以为已经通过了，后面再次测试发现又出问题了，又修 bug，这就是并发 bug😆。

完整代码

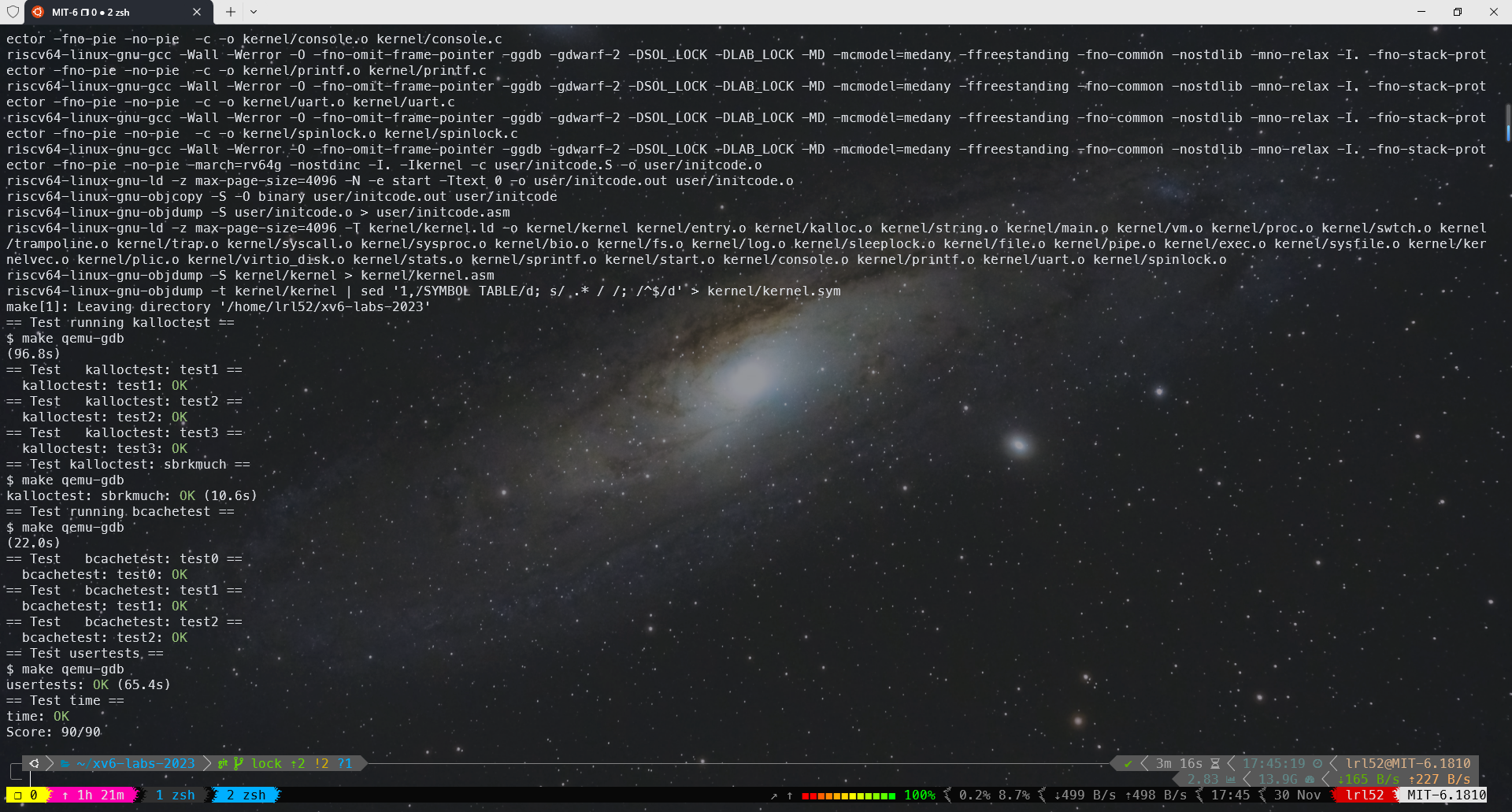
最后完整代码实现如下，这个是实现经过了多次反复测试，应该没有任何 BUG 了：

diff --git a/kernel/bio.c b/kernel/bio.c
index 60d91a6..d08c193 100644
--- a/kernel/bio.c
+++ b/kernel/bio.c
@@ -24,7 +24,9 @@
 #include "buf.h"

 struct {
-  struct spinlock lock;
+  struct spinlock lock[NBUF]; // block the later one when two threads that
+                              // get the same blockno are concrrently searching
+                              // for a uncached block.
   struct buf buf[NBUF];

   // Linked list of all buffers, through prev/next.
@@ -33,22 +35,24 @@ struct {
   struct buf head;
 } bcache;

+static char bcache_lock_name[NBUF][10];
+
+#define MULTIPLIER 2654435769U  // Knuth's multiplicative method
+
+static unsigned int hash(unsigned int k) {
+    return (unsigned int)(((uint64)k * MULTIPLIER) >> 28) % NBUF;
+}
+
 void
 binit(void)
 {
-  struct buf *b;
+  int i;

-  initlock(&bcache.lock, "bcache");
-
-  // Create linked list of buffers
-  bcache.head.prev = &bcache.head;
-  bcache.head.next = &bcache.head;
-  for(b = bcache.buf; b < bcache.buf+NBUF; b++){
-    b->next = bcache.head.next;
-    b->prev = &bcache.head;
-    initsleeplock(&b->lock, "buffer");
-    bcache.head.next->prev = b;
-    bcache.head.next = b;
+  for (i = 0; i < NBUF; ++i) {
+    snprintf(bcache_lock_name[i], sizeof(bcache_lock_name[i]), "bcache%d", i);
+    initlock(&bcache.buf[i].spinlock, bcache_lock_name[i]);
+    initlock(&bcache.lock[i], bcache_lock_name[i]);
+    initsleeplock(&bcache.buf[i].lock, "buffer");
   }
 }

@@ -59,32 +63,58 @@ static struct buf*
 bget(uint dev, uint blockno)
 {
   struct buf *b;
+  int idx, i, j;

-  acquire(&bcache.lock);
+  idx = hash(blockno);

   // Is the block already cached?
-  for(b = bcache.head.next; b != &bcache.head; b = b->next){
-    if(b->dev == dev && b->blockno == blockno){
-      b->refcnt++;
-      release(&bcache.lock);
+  for (i = idx, j = 0; j < NBUF; i = (i + 1) % NBUF, ++j) {
+    b = &bcache.buf[i];
+    acquire(&b->spinlock);
+    if (b->dev == dev && b->blockno == blockno) {
+      ++b->refcnt;
+      release(&b->spinlock);
       acquiresleep(&b->lock);
       return b;
     }
+    release(&b->spinlock);
   }

   // Not cached.
-  // Recycle the least recently used (LRU) unused buffer.
-  for(b = bcache.head.prev; b != &bcache.head; b = b->prev){
-    if(b->refcnt == 0) {
+  // Search for an unused buffer.
+
+  // Consider the case when two threads are searching for the same uncached block,
+  // the later one should wait for the former one to finish the allocation. Otherwise,
+  // the later one may encounter an empty buffer ealier than the former one.
+  // So we block the later one until the former one finishes allocation.
+  acquire(&bcache.lock[idx]);
+
+  for (i = idx, j = 0; j < NBUF; i = (i + 1) % NBUF, ++j) {
+    b = &bcache.buf[i];
+    acquire(&b->spinlock);
+
+    // The former thread may have already allocated the buffer.
+    if (b->dev == dev && b->blockno == blockno) {
+      ++b->refcnt;
+      release(&b->spinlock);
+      release(&bcache.lock[idx]);
+      acquiresleep(&b->lock);
+      return b;
+    }
+
+    if (b->refcnt == 0) {
       b->dev = dev;
       b->blockno = blockno;
       b->valid = 0;
       b->refcnt = 1;
-      release(&bcache.lock);
+      release(&b->spinlock);
+      release(&bcache.lock[idx]);
       acquiresleep(&b->lock);
       return b;
     }
+    release(&b->spinlock);
   }
+
   panic("bget: no buffers");
 }

@@ -121,33 +151,23 @@ brelse(struct buf *b)

   releasesleep(&b->lock);

-  acquire(&bcache.lock);
-  b->refcnt--;
-  if (b->refcnt == 0) {
-    // no one is waiting for it.
-    b->next->prev = b->prev;
-    b->prev->next = b->next;
-    b->next = bcache.head.next;
-    b->prev = &bcache.head;
-    bcache.head.next->prev = b;
-    bcache.head.next = b;
-  }
-
-  release(&bcache.lock);
+  acquire(&b->spinlock);
+  --b->refcnt;
+  release(&b->spinlock);
 }

 void
 bpin(struct buf *b) {
-  acquire(&bcache.lock);
-  b->refcnt++;
-  release(&bcache.lock);
+  acquire(&b->spinlock);
+  ++b->refcnt;
+  release(&b->spinlock);
 }

 void
 bunpin(struct buf *b) {
-  acquire(&bcache.lock);
-  b->refcnt--;
-  release(&bcache.lock);
+  acquire(&b->spinlock);
+  --b->refcnt;
+  release(&b->spinlock);
 }


diff --git a/kernel/buf.h b/kernel/buf.h
index 4616e9e..4b79b5f 100644
--- a/kernel/buf.h
+++ b/kernel/buf.h
@@ -4,9 +4,8 @@ struct buf {
   uint dev;
   uint blockno;
   struct sleeplock lock;
+  struct spinlock spinlock; // protect other fields except data
   uint refcnt;
-  struct buf *prev; // LRU cache list
-  struct buf *next;
   uchar data[BSIZE];
 };

测试

image-20241130174535914

References

Donald E. Knuth, The Art of Computer Programming, Volume 3: Sorting and Searching.

暂无评论

发送评论 编辑评论 


				

			

						

				

					

						

							

								
							

							
						

					

				

				

					

						

							

								
							

							
						

					

				

				

					

						

							

								
							

							
							
													

					

				

			

			
			

				

					
				

			

				

											

							
							
						

																

							
							
						

																

							
							
						

										
					
											
						

	

		
|´・ω・)ノ
ヾ(≧∇≦*)ゝ
(☆ω☆)
（╯‵□′）╯︵┴─┴
￣﹃￣
(/ω＼)
∠( ᐛ 」∠)＿
(๑•̀ㅁ•́ฅ)
→_→
୧(๑•̀⌄•́๑)૭
٩(ˊᗜˋ*)و
(ノ°ο°)ノ
(´இ皿இ｀)
⌇●﹏●⌇
(ฅ´ω`ฅ)
(╯°A°)╯︵○○○
φ(￣∇￣o)
ヾ(´･ ･｀｡)ノ"
( ง ᵒ̌皿ᵒ̌)ง⁼³₌₃
(ó﹏ò｡)
Σ(っ °Д °;)っ
( ,,´･ω･)ﾉ"(´っω･｀｡)
╮(╯▽╰)╭
o(*////▽////*)q
＞﹏＜
( ๑´•ω•) "(ㆆᴗㆆ)
😂
😀
😅
😊
🙂
🙃
😌
😍
😘
😜
😝
😏
😒
🙄
😳
😡
😔
😫
😱
😭
💩
👻
🙌
🖕
👍
👫
👬
👭
🌚
🌝
🙈
💊
😶
🙏
🍦
🍉
😣
Source: github.com/k4yt3x/flowerhd
	

	

		
颜文字
Emoji
小恐龙
花!
	


									

			

			
			
		

	






上一篇
下一篇